Biểu đồ dưới đây biểu diễn kết quả khảo sát thành tích chạy $100$ m của một số học sinh.

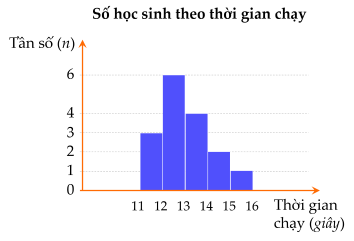
a) Có bao nhiêu học sinh chạy $100$ m hết ít hơn $13$ giây?

b) Có tổng số bao nhiêu học sinh tham gia khảo sát?

Ba bạn Bích, Cường, Dung được xếp ngẫu nhiên trên một hàng ghế có ba chỗ ngồi. Tính xác suất của biến cố: "Cường và Dung không ngồi cạnh nhau".

Cho hai biểu thức $A=\dfrac{\sqrt{x}+2}{\sqrt{x}}$ và $B=\dfrac{x}{x-4}+\dfrac{1}{\sqrt{x}-2}+\dfrac{1}{\sqrt{x}+2}$ với $x>0, \, x \ne 4$.

1) Tính giá trị của biểu thức $A$ với $x = 36$.

2) Rút gọn biểu thức $B.$

3) Cho $P=\dfrac{A}{B}$. Tìm $x$ thỏa mãn: $x.P \le 10\sqrt{x}-29-\sqrt{x-25}$.

Bác Nga chia số tiền $600$ triệu đồng của mình cho hai khoản đầu tư. Sau một năm, tổng số tiền lãi bác thu được là $51,5$ triệu đồng. Lãi suất cho khoản đầu tư thứ nhất là $8\%$/năm và khoản đầu tư thứ hai là $9\%$/năm. Tính số tiền bác Nga đầu tư cho mỗi khoản.

Một tổ sản xuất phải làm xong $4\,800$ sản phẩm trong một số ngày quy định. Thực tế, mỗi ngày tổ đó đã làm được nhiều hơn $100$ sản phẩm so với số sản phẩm phải làm trong $1$ ngày theo kế hoạch. Vì thế $8$ ngày trước khi hết thời hạn, tổ sản xuất đã làm xong $4\,800$ sản phẩm. Theo kế hoạch, mỗi ngày tổ sản xuất phải làm bao nhiêu sản phẩm? (Giả định rằng số sản phẩm mà mỗi tổ làm được trong mỗi ngày là bằng nhau).

Biết rằng phương trình bậc hai $x^2-5x+a=0$ có một nghiệm là $x=\dfrac{5-\sqrt{41}}{2}$. Tính tổng bình phương hai nghiệm của phương trình trên.

Một đống cát dạng hình nón có chu vi đáy là $8\pi$ (m) và chiều cao là $1,6$ (m).

a) Tính thể tính của đống cát (lấy $\pi =3,14$ và kết quả làm tròn đến hàng phần trăm).

b) Người ta dùng xe cải tiến để chở đống cát đó đi, biết thùng chở của xe cải tiến là dạng hình hộp chữ nhật có kích thước rộng $1$(m), dài $1,2$ (m) và cao $50$ (cm). Mỗi chuyến chở, người ta chỉ gạt tới miệng thùng chở của xe để cát không bị rơi ra ngoài. Vậy phải chở bao nhiêu chuyến thì mới hết đống cát đó?

Cho tam giác $ABC$ có ba góc nhọn, $AB\lt AC$ và tam giác này nội tiếp đường tròn $(O;R)$. Kẻ ba đường cao $AD$, $BE$, $CF$ cắt nhau tại $H$.

a) Chứng minh bốn điểm $B$, $F$, $E$, $C$ cùng thuộc một đường tròn.

b) Đường thẳng $EF$ cắt đường thẳng $BC$ tại $K$. Chứng minh $KE.KF=KB.KC$.

c) Gọi $I$ là tâm của đường tròn ngoại tiếp tứ giác $BFEC$ và $M$ là giao điểm của $AK$ và đường tròn $(O;R)$. Chứng minh $\widehat{KAC} = \widehat{KFM}$ và ba điểm $M$, $H$, $I$ thẳng hàng.

Một doanh nghiệp chuyên kinh doanh sản phẩm của Apple. Hiện nay, doanh nghiệp đang tập trung chiến lược kinh doanh điện thoại Iphone 16 Plus với chi phí mua vào là $23$ triệu đồng và bán ra với giá $27$ triệu đồng mỗi chiếc. Với giá bán này thì số lượng điện thoại mà khách hàng mua trong một tháng là $600$ chiếc. Nhằm mục tiêu đẩy mạnh hơn nữa lượng tiêu thụ dòng điện thoại đang bán chạy này, doanh nghiệp dự định giảm giá bán và ước tính rằng: theo tỉ lệ cứ giảm $100$ nghìn đồng mỗi chiếc điện thoại thì số lượng điện thoại bán ra trong mỗi tháng sẽ tăng thêm $20$ chiếc. Vậy doanh nghiệp phải bán ra với giá mới là bao nhiêu để sau khi giảm giá lợi nhuận thu được sẽ cao nhất?