Đề khảo sát chất lượng Toán 12 năm 2024

Câu 1 (1đ):

Bất phương trình $\Big(\dfrac13 \Big)^{x^2-3x} \ge 1$ có tất cả bao nhiêu nghiệm nguyên?

3

.

4

.

2

.

1

.

Câu 2 (1đ):

Trong không gian $Oxyz$ , cho hai điểm $A(1;2;-1)$ và $B(2;4;1)$ . Trọng tâm của tam giác $OAB$ có tọa độ là

(3;6;0)

.

(-1;-2;0)

.

(1;3;0)

.

(1;2;0)

.

Câu 3 (1đ):

Bảng thống kê dưới đây cho biết thu nhập bình quân đầu người/tháng của người dân Hà Nội (tính theo triệu đồng) trong giai đoạn từ năm 2018 đến năm 2024:

Năm	Thu nhập (triệu đồng/tháng)
2018	$5,901$
2019	$6,403$
2020	$6,203$
2021	$6,002$
2022	$6,423$
2023	$6,896$
2024	$7,546$

Mẫu số liệu thống kê trên có khoảng biến thiên bằng bao nhiêu (tính theo triệu đồng)?

2,290

.

2,660

.

1,645

.

0,867

.

Câu 4 (1đ):

Trong không gian

Oxyz

, phương trình mặt phẳng đi qua điểm

M(1;-2;3)

và có vectơ pháp tuyến

\overrightarrow{n}=(2;0;1)

là

2x+z-5=0

.

2y+z+1=0

.

x-2y+3z-5=0

.

2x+y=0

.

Câu 5 (1đ):

Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác vuông cân tại $A$ . Gọi các điểm $M,\,N$ lần lượt là trung điểm của $SB$ và $SC$ . Khi đó góc giữa hai đường thẳng $MN$ và $AB$ bằng

90^\circ

.

30^\circ

.

45^\circ

.

60^\circ

.

Câu 6 (1đ):

Nếu

\displaystyle \int _{0}^{2}f(x)\mathrm{d}x=3

thì

\displaystyle \int _{0}^{2}[ f(x)+2 ]\mathrm{d}x

bằng

5

.

10

.

7

.

6

.

Câu 7 (1đ):

Tiệm cận xiên của đồ thị hàm số

y=x-1-\dfrac{2}{x+1}

là đường thẳng có phương trình

y=x+1

.

y=-x-1

.

y=-x+1

.

y=x-1

.

Câu 8 (1đ):

Cân nặng (kg) của $50$ quả mít trong đợt thu hoạch của một trang trại được thống kê trong bảng dưới đây:

Cân nặng (kg)	Số quả mít
$[4;6)$	$6$
$[6;8)$	$12$
$[8;10)$	$19$
$[10;12)$	$9$
$[12;14)$	$4$

Khối lượng trung bình của $50$ quả mít trên bằng

9,12

kg.

8,82

kg.

8,52

kg.

8,72

kg.

Câu 9 (1đ):

Cho hàm số bậc ba $y=f(x)$ có đồ thị như hình vẽ.

Cho hàm số bậc ba $y=f(x)$ có đồ thị như hình vẽ

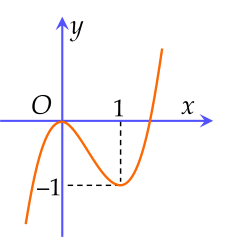
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?

(-\infty ;0)

.

(1;+\infty)

.

(-\infty ;+\infty)

.

(0;1)

.

Câu 10 (1đ):

Cho khối lăng trụ đứng

ABC.A'B'C'

có đáy

ABC

là tam giác vuông cân tại

A

,

AB=AC=1, \, AA'=2

. Thể tích khối lăng trụ đã cho bằng

2

.

1

.

\dfrac{2}{3}

.

\dfrac{1}{3}

.

Câu 11 (1đ):

Cho cấp số nhân

(u_n)

với

u_3=8

và công bội

q=-2

. Giá trị của

u_2

bằng

-16

.

-4

.

10

.

6

.

Câu 12 (1đ):

Nguyên hàm của hàm số

f(x)=3^x

là

3^x. \ln 3+C

3^x+C

.

\dfrac{3^x}{\ln 3}+C

.

\dfrac{3^{x+1}}{x+1}+C

.

Câu 13 (1đ):

Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình chữ nhật và cạnh $SA$ vuông góc với mặt phẳng đáy. Biết $AB=1, \, AD=2$ và $SA=3$ . Xét hệ trục tọa độ $Oxyz$ với $O$ trùng $A$ , các tia $Ox$ , $Oy,\,Oz$ lần lượt trùng với các tia $AB,\,AD,\,AS$ (như hình vẽ).

Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình chữ nhật và cạnh $SA$ vuông góc với mặt phẳng đáy

(Nhấp vào ô màu vàng để chọn đúng / sai)

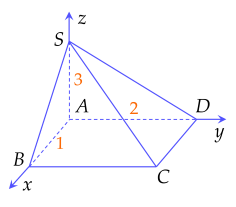
a) Tọa độ điểm $C$ là $(1;2;0)$ .
b) $[\overrightarrow{SC},\overrightarrow{BD}]=(6;-3;4)$ .
c) Gọi $(P)$ là mặt phẳng chứa đường thẳng $SC$ và song song với đường thẳng $BD$ . Phương trình mặt phẳng $(P)$ là $6x+3y+4z-12=0$ .
d) Khoảng cách giữa đường thẳng $BD$ và mặt phẳng $(P)$ bằng $\dfrac{6}{61}$ .

Câu 14 (1đ):

Cho hàm số $f(x)=\mathrm{e}^{2x}-2x$ .

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Hàm số có tập xác định là $\mathbb{R}$ .
b) Đạo hàm của hàm số đã cho là $f'(x)=2\mathrm{e}^{2x}-2$ .
c) Tập nghiệm của bất phương trình $f'(x)>0$ là $S=(0;+\infty)$ .
d) Hàm số đã cho có giá trị cực tiểu bằng $0$ .

Câu 15 (1đ):

Một chất điểm chuyển động thẳng trong $19$ giây với vận tốc $v(t)$ (đơn vị: m/s) là hàm số phụ thuộc thời gian $t$ (đơn vị: giây) có đồ thị như hình vẽ.

Một chất điểm chuyển động thẳng trong $19$ giây với vận tốc $v(t)$ (đơn vị: m/s) là hàm số phụ thuộc thời gian $t$

(Nhấp vào ô màu vàng để chọn đúng / sai)

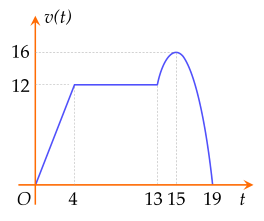
a) Tại thời điểm $t=19$ giây, vận tốc của chất điểm bằng $16$ m/s.
b) Quãng đường chất điểm đi được trong khoảng thời gian từ $0$ giây đến $4$ giây bằng $24$ m.
c) Trong khoảng thời gian từ $13$ giây đến $19$ giây, đồ thị của $v(t)$ là một phần của đường parabol. Khi đó $v(t)=-t^2+30t-209$ m/s.
d) Quãng đường chất điểm đi được từ lúc xuất phát đến khi dừng lại bằng $204$ m.

Câu 16 (1đ):

Trong một trò chơi, con ngựa của bạn Toàn đang đứng ở vị trí xuất phát (như hình vẽ).

Trong một trò chơi, con ngựa của bạn Toàn đang đứng ở vị trí xuất phát (như hình vẽ)

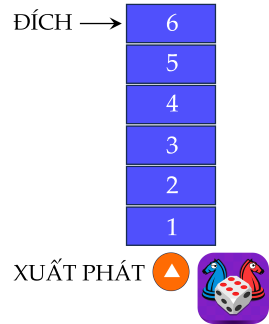
Luật chơi như sau: Để di chuyển con ngựa, bạn Toàn cần gieo một con xúc xắc có sáu mặt cân đối, đồng chất. Ở mỗi lượt chơi, bạn có tối đa ba lần gieo. Ở lần gieo thứ nhất, con ngựa di chuyển đến ô có số thứ tự bằng số tương ứng với số chấm gieo được của con xúc xắc. Từ những lần gieo sau, nếu tổng của số tương ứng với số chấm gieo được của con xúc xắc và số tương ứng ghi ở ô con ngựa đang đứng lớn hơn $6$ thì con ngựa sẽ đứng yên, còn nếu tổng này nhỏ hơn hoặc bằng $6$ thì con ngựa được di chuyển số ô bằng số chấm gieo được. Con ngựa này gọi là về đích nếu nó đến được ô số $6$ .

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Xác suất để con ngựa về đích ở lần gieo thứ nhất bằng $\dfrac{1}{6}$ .
b) Xác suất để con ngựa về đích ở lần gieo thứ hai bằng $\dfrac{5}{36}$ .
c) Xác suất để con ngựa về đích ở lần gieo thứ ba và trong cả ba lần gieo con ngựa đều được di chuyển bằng $\dfrac{5}{108}$ .
d) Xác suất để con ngựa về đích sau nhiều nhất ba lần gieo bằng $\dfrac{19}{54}$ .

Câu 17 (1đ):

Anh Thắng có $500$ triệu đồng và đã vay thêm ngân hàng $400$ triệu đồng với lãi suất $8\%$ /năm theo thể thức lãi kép, kì hạn $1$ năm. Anh Thắng đã dùng toàn bộ $900$ triệu đồng này để mua một mảnh đất với giá $20$ triệu đồng m². Sau đúng $2$ năm, anh bán mảnh đất đó với giá $29$ triệu đồng m² và dùng số tiền thu được trả hết nợ cho ngân hàng. Sau khi trả nợ xong, anh được lãi bao nhiêu triệu đồng so với tiền vốn anh có ban đầu (kết quả làm tròn đến hàng đơn vị)?

Trả lời:

Câu 18 (1đ):

Một cửa vòm có dạng hình parabol được lắp các tấm kính hình tròn đường kính $1m$ và các tấm kính hình vuông có cạnh $1$ m như hình vẽ.

Một cửa vòm có dạng hình parabol được lắp các tấm kính hình tròn đường kính $1m$ và các tấm kính hình vuông có cạnh $1$ m như hình vẽ

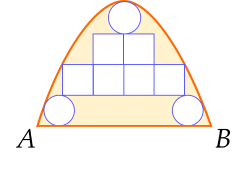
Phần còn lại của cửa được sơn màu trang trí với mức giá $1,2$ triệu đồng/m². Chi phí sơn màu là bao nhiêu triệu đồng (kết quả làm tròn đến hàng phần chục)?

Trả lời:

Câu 19 (1đ):

Một đại lý nhập khẩu trái cây tươi để phân phối cho các cửa hàng. Mỗi lần nhập khẩu trái cây, khoán chi phí vận chuyển (không đổi) là $25$ triệu đồng. Chi phí bảo quản mỗi tạ trái cây dự trũ trong kho là $80$ nghìn đồng/ngày. Thời gian bảo quản trái cây trong kho tối đa $10$ ngày. Biết rằng, kể từ ngày đầu tiên nhập hàng, đại lý sẽ phân phối tới các cửa hàng $25$ tạ trái cây mỗi ngày. Mỗi lần nhập hàng, đại lý phải nhập đủ trái cây cho bao nhiêu ngày phân phối để chi phí trung bình cho mỗi ngày thấp nhất (bao gồm chi phí vận chuyển và chi phí bảo quản trong kho)?

Trả lời:

Câu 20 (1đ):

Cho hình chóp tam giác $S.ABC$ có đáy $ABC$ là tam giác vuông tại $B$ , cạnh bên $SA$ vuông góc với mặt phẳng đáy. Biết $AB=1$ , $BC= \sqrt{2}$ và $[S,BC,A]=45^\circ$ . Góc giữa đường thẳng $SC$ và mặt phẳng $(ABC)$ bằng bao nhiêu độ?

Trả lời:

Câu 21 (1đ):

Trạm kiểm soát không lưu đang theo dõi hai máy bay. Giả sử trong không gian với hệ trục tọa độ $Oxyz$ , đơn vị đo lấy theo kilômét, tại cùng một thời điểm theo dõi ban đầu: máy bay thứ nhất ở tọa độ $A(0;35;10)$ , bay theo hướng vector $\overrightarrow{u_1} = (3;4;0)$ , với tốc độ không đổi $900$ km/h và máy bay thứ hai ở tọa độ $B(31;10;11)$ , bay theo hướng $\overrightarrow{u_2} = (5;12;0)$ với tốc độ không đổi $910$ (km/h). Biết khoảng cách an toàn tối thiểu giữa hai máy bay là $5$ hải lý (khoảng $9,3$ km). Nếu hai máy bay tiếp tục di chuyển với tốc độ bay như trên thì sau ít nhất bao nhiêu phút (kể từ thời điểm theo dõi ban đầu), hai máy bay vi phạm khoảng cách an toàn (kết quả làm tròn đến hàng phần trăm)?

Trả lời:

Câu 22 (1đ):

Đồ thị hàm số $y = \dfrac{x^2}{x + 1}$ có hai điểm cực trị $A$ và $B$ . Độ dài đoạn thẳng $AB$ bằng bao nhiêu (kết quả làm tròn đến hàng phần chục)?

Trả lời:

Bài học cùng chủ đề

Đề khảo sát chất lượng Toán 12 năm 2024 – 2025 sở GD&ĐT Hà Nội SVIP

Yêu cầu đăng nhập!

Bài học cùng chủ đề

Báo cáo học liệu

Mua học liệu

Mua học liệu:

Số dư ví của bạn: 0 coin - 0 Xu

Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu

Để nhận Coin\Xu, bạn có thể:

Chi tiết xem tại đây

Thông tin của bạn

Đề khảo sát chất lượng Toán 12 năm 2024 – 2025 sở GD&ĐT Hà Nội SVIP

Yêu cầu đăng nhập!

Truy vết IP log

Báo lỗi câu hỏi

Các khóa học có thể bạn quan tâm

Yêu cầu VIP