Tóm tắt kiến thức trọng tâm chuyên đề Diện tích hình phẳng ứng dụng tích phân

Câu 1 (1đ):

Cho hàm số $y=f\left(x \right)$ xác định và liên tục trên đoạn. Diện tích hình phẳng giới hạn bởi đồ thị hàm số $y=f\left(x \right)$ , trục hoành và hai đường thẳng $x=a,\,x=b$ được tính theo công thức nào?

\displaystyle\int\limits_{b}^{a}{\left| f\left(x \right) \right|}dx

.

\displaystyle\int\limits_{a}^{b}{\left| f\left(x \right) \right|}dx

.

\left| \displaystyle\int\limits_{a}^{b}{f\left(x \right)}dx \right|

.

\displaystyle\int\limits_{a}^{b}{f\left(x \right)}dx

.

Câu 2 (1đ):

Cho hàm số $y=f\left(x \right)$ và $y=g\left(x \right)$ có đồ thị như hình vẽ:

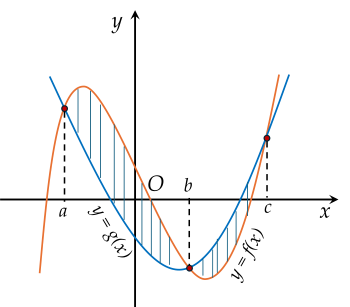
loading...

Diện tích $S$ của phần gạch chéo trong hình vẽ trên được tính bằng công thức là

S=\displaystyle\int\limits_{a}^{c}{\left| f\left(x \right)-g\left(x \right) \right|dx}

.

S=\displaystyle\displaystyle\left| \int\limits_{a}^{c}{\left[ f\left(x \right)-g\left(x \right) \right]dx} \right|

.

S=\displaystyle\int\limits_{a}^{c}{\left[ g\left(x \right)-f\left(x \right) \right]dx}

.

S=\displaystyle\int\limits_{a}^{c}{\left[ f\left(x \right)-g\left(x \right) \right]dx}

.

Câu 3 (1đ):

Diện tích hình phẳng $\left(H \right)$ được giới hạn bởi đồ thị hàm số $y=f\left(x \right)$ , trục hoành và hai đường thẳng $x=a,\,x=b$ $\left(a<b \right)$ (phần gạch chéo như hình vẽ) được tính theo công thức nào?

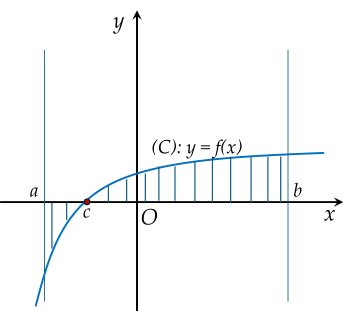
loading...

S=-\displaystyle\int\limits_{a}^{c}{f\left(x \right)}dx+\displaystyle\int\limits_{c}^{b}{f\left(x \right)}dx

.

S=\displaystyle\int\limits_{a}^{c}{f\left(x \right)}dx+\displaystyle\int\limits_{c}^{b}{f\left(x \right)}dx

.

S=\displaystyle\int\limits_{a}^{b}{f\left(x \right)}dx

.

S=\left|\displaystyle \int\limits_{a}^{b}{f\left(x \right)}dx \right|

.

Câu 4 (1đ):

Diện tích $S$ hình phẳng giới hạn bởi các đường $y=2{{x}^{2}}$ , $y=-1$ , $x=0$ và $x=1$ là

S=\dfrac{47}{15}

.

S=\dfrac{5}{3}

.

S=\dfrac{1}{3}

.

S=\dfrac{5\pi }{3}

.

Câu 5 (1đ):

Cho hình phẳng $\left(D \right)$ giới hạn bởi đồ thị của ba hàm số $y=f(x)$ , $y=g(x)$ , $y=h(x)$ như hình bên dưới:

loading...

Diện tích hình phẳng $\left(D \right)$ là

S=\displaystyle\int\limits_{a}^{c}{\left[ f(x)-g(x) \right]dx}

.

S=\displaystyle\int\limits_{a}^{b}{\left[ f(x)-h(x) \right]dx}+\displaystyle\int\limits_{b}^{c}{\left[ g(x)-h(x) \right]dx}

.

S=\displaystyle\int\limits_{a}^{b}{\left[ f(x)-g(x) \right]dx}+\displaystyle\int\limits_{b}^{c}{\left[ g(x)-h(x) \right]dx}

.

S=\displaystyle\int\limits_{a}^{b}{\left[ f(x)-g(x) \right]dx}-\displaystyle\int\limits_{b}^{c}{\left[ g(x)-h(x) \right]dx}

.

Câu 6 (1đ):

Diện tích của hình phẳng được giới hạn bởi đồ thị hàm số $y=f(x)$ , trục hoành và hai đường thẳng $x=a$ , $x=b$ ( $a\lt b$ ) tính theo công thức nào dưới đây?

S= \displaystyle\int\limits_{a}^{c} f(x)\,\mathrm{d}x+\displaystyle\int\limits_{c}^{b} f(x)\,\mathrm{d}x

.

S= \left|\displaystyle\int\limits_{a}^{b} f(x)\,\mathrm{d}x\right|

.

S= -\displaystyle\int\limits_{a}^{c} f(x)\,\mathrm{d}x+\displaystyle\int\limits_{c}^{b} f(x)\,\mathrm{d}x

.

S= \displaystyle\int\limits_{a}^{b} f(x)\,\mathrm{d}x

.

Câu 7 (1đ):

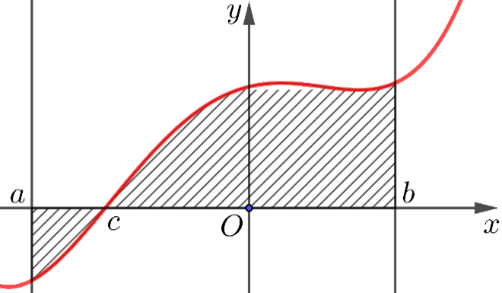
Cho đồ thị $y=f(x)$ như hình vẽ bên. Công thức diện tích miền được gạch sọc ở hình bên là

.

\displaystyle\int\limits_{-1}{2} (-x^2+3)\,\mathrm{d}x

.

\displaystyle\int\limits_{-1}{2} (2x^2-2x-4)\,\mathrm{d}x

.

\displaystyle\int\limits_{-1}{2} (x^2-2x-1)\,\mathrm{d}x

.

\displaystyle\int\limits_{-1}{2} (-2x^2+2x+4)\,\mathrm{d}x

.

Câu 8 (1đ):

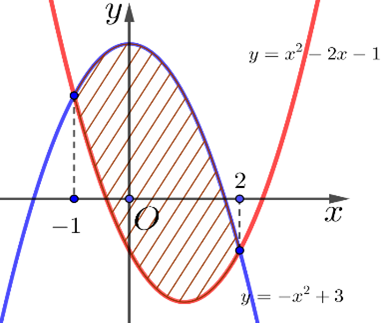
Diện tích hình phẳng được giới hạn bởi đồ thị hàm số $y=\sqrt[3]{x}$ , trục hoành và hai đường thẳng $x=1$ , $x=8$ là

\dfrac{45}{7}

.

\dfrac{45}{4}

.

\dfrac{45}{8}

.

\dfrac{45}{2}

.

Câu 9 (1đ):

Cho hình phẳng $(H)$ giới hạn bởi đồ thị của hàm số $f_1(x)$ và $f_2(x)$ liên tục trên $[a ;\,b]$ và đường thẳng $x=a$ , $x=b$ . Công thức tính diện tích của hình $(H)$ là

\displaystyle\int\limits_{a}^{c_1} \big(f_2(x)-f_1(x)\big)\,\mathrm{d}x+ \displaystyle\int\limits_{c_1}^{c_2} \big(f_1(x)-f_2(x)\big)\,\mathrm{d}x+ \displaystyle\int\limits_{c_2}^{b} \big(f_2(x)-f_1(x)\big)\,\mathrm{d}x

.

\displaystyle\int\limits_{a}^{c_1} \big(f_1(x)-f_2(x)\big)\,\mathrm{d}x+ \displaystyle\int\limits_{c_1}^{c_2} \big(f_1(x)-f_2(x)\big)\,\mathrm{d}x+ \displaystyle\int\limits_{c_2}^{b} \big(f_1(x)-f_2(x)\big)\,\mathrm{d}x

.

\displaystyle\int\limits_{a}^{c_1} \big(f_1(x)-f_2(x)\big)\,\mathrm{d}x+ \displaystyle\int\limits_{c_1}^{c_2} \big(f_2(x)-f_1(x)\big)\,\mathrm{d}x+ \displaystyle\int\limits_{c_2}^{b} \big(f_1(x)-f_2(x)\big)\,\mathrm{d}x

.

\displaystyle\int\limits_{a}^{b} \big(f_1(x)-f_2(x)\big)\,\mathrm{d}x

.

Câu 10 (1đ):

Gọi $S$ là diện tích của hình phẳng giới hạn bởi các đường $y=2^x$ , $y=1$ , $x=0$ , $x=2$ . Mệnh đề nào dưới đây sai?

S=\displaystyle\int\limits_{0}^{2} (1-2^x)\,\mathrm{d}x

.

S=\displaystyle\int\limits_{0}^{2} |1-2^x|\,\mathrm{d}x

.

S=\displaystyle\int\limits_{0}^{2} (2^x-1)\,\mathrm{d}x

.

S=\displaystyle\int\limits_{0}^{2} |2^x-1|\,\mathrm{d}x

.

Câu 11 (1đ):

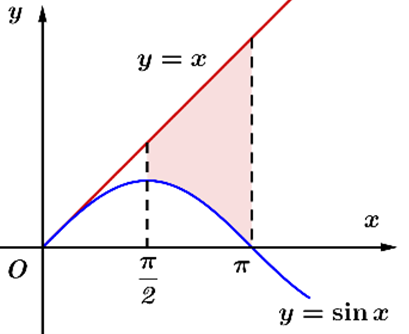
Diện tích hình phẳng giới hạn bởi các đường $y=\sin x$ , $y=x$ , $x=\dfrac{\pi}{2}$ , $x=\pi$ là

\dfrac{3\pi^2}{8}-1

.

\dfrac{3\pi^2}{8}+1

.

\dfrac{2\pi^2}{3}+1

.

\dfrac{2\pi^2}{3}-1

.

Câu 12 (1đ):

Giá trị của $a$ để diện tích $S$ của hình phẳng giới hạn bởi $(P): y=\dfrac{x^2-2x}{x-1}$ , đường thẳng $d: y=x-1$ và $x=a$ ,

$x=2a$ ( $a>1$ ) bằng $\ln3$ là

2

.

3

.

4

.

1

.

Câu 13 (1đ):

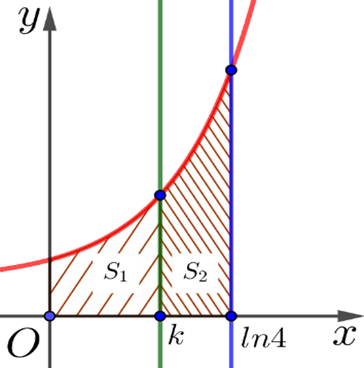
Cho hình thang cong $(H)$ giới hạn bởi các đường $y=e^x$ , $y=0$ , $x=0$ , $x=\ln4$ . Đường thẳng $x=k$ ( $0\lt k\lt \ln4$ ) chia $(H)$ thành hai phần có diện tích là $S_1$ và $S_2$ như hình vẽ. Giá trị của $k$ để $S_1=2S_2$ là

2

.

3

.

\ln3

.

\ln2

.

Câu 14 (1đ):

Diện tích hình phẳng giới hạn bởi đồ thị hàm số $y=\cos x$ , trục tung, trục hoành và đường thẳng $x=\pi$ bằng $1$ .

4

.

2

.

3

.

1

.

Câu 15 (1đ):

Cho hàm số $f(x)=-x^2+4$ và $g(x)=x-1$ . Xét tính đúng, sai của các mệnh đề sau:

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Diện tích hình phẳng $(H_1)$ tạo bởi $f(x)$ , $Ox$ và hai đường thẳng $x=-3$ , $x=3$ là $S_{(H_1)}=\displaystyle\int\limits_{-3}^{3} \|f(x)\|\,\mathrm{d}x=\dfrac{46}{3}$ .
b) Diện tích hình phẳng $(H_2)$ tạo bởi $f(x)$ , $Ox$ và hai đường thẳng $x=-2$ , $x=2$ là $S_{(H_2)}=\displaystyle\int\limits_{-2}^{2} f(x)\,\mathrm{d}x=\dfrac{32}{3}$ .
c) Diện tích hình phẳng $(H_3)$ tạo bởi $g(x)$ , $Ox$ và hai đường thẳng $x=-3$ , $x=3$ là $S_{(H_3)}=\left\|\displaystyle\int\limits_{-3}^{1} g(x)\,\mathrm{d}x + \displaystyle\int\limits_{1}^{3} g(x)\,\mathrm{d}x\right\|=6$ .
d) Diện tích hình phẳng $(H_4)$ tạo bởi $g(x)$ , $Ox$ và hai đường thẳng $x=-3$ , $x=3$ là $S_{(H_4)}= -\displaystyle\int\limits_{-3}^{1} g(x)\,\mathrm{d}x + \displaystyle\int\limits_{1}^{3} g(x)\,\mathrm{d}x=10$ .

Bài học cùng chủ đề

Dạng 1. Diện tích hình phẳng SVIP

Yêu cầu đăng nhập!

Bài học cùng chủ đề

Báo cáo học liệu

Mua học liệu

Mua học liệu:

Số dư ví của bạn: 0 coin - 0 Xu

Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu

Để nhận Coin\Xu, bạn có thể:

Chi tiết xem tại đây

Thông tin của bạn

Dạng 1. Diện tích hình phẳng SVIP

Tải đề xuống bằng file Word

Yêu cầu đăng nhập!

Truy vết IP log

Báo lỗi câu hỏi

Các khóa học có thể bạn quan tâm

Yêu cầu VIP