Đề kiểm tra học kì I (đề số 3)

Câu 1 (1đ):

Cho hàm số $y=f(x)$ có đồ thị là đường cong như hình vẽ:

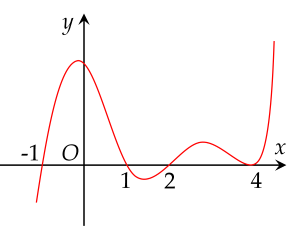
loading...

Hàm số đã cho nghịch biến trên khoảng nào dưới đây?

(-\infty ;\,-1)

.

(0;\,1)

.

(1;\,2)

.

(-1;\,1).

Câu 2 (1đ):

Cho hàm số $y=x^4-\dfrac23x^3-x^2.$ Mệnh đề nào sau đây đúng?

Hàm số chỉ có một giá trị cực tiểu.

Hàm số có giá trị cực tiểu là

0

.

Hàm số có giá trị cực tiểu là

-\dfrac23

và giá trị cực đại là

-\dfrac{5}{48}

.

Hàm số có hai giá trị cực tiểu là

-\dfrac23

và

-\dfrac{5}{48}

.

Câu 3 (1đ):

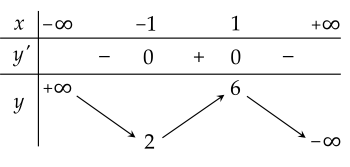
loading...

Hình vẽ trên là bảng biến thiên của hàm số nào sau đây?

y=\dfrac{x+1}{x-1}

.

y=x^4-2x^2-3

.

y=-x^3+3x+4

.

y=x^3-3x+4

.

Câu 4 (1đ):

Trong không gian $Oxyz$ , cho hai vectơ $\overrightarrow{u}=(-1 ; 1 ; 3)$ và $\overrightarrow{v}=(-2 ; 1 ;-3)$ . Giá trị của $|2 \overrightarrow{u}-3 \overrightarrow{v}|$ là

\sqrt{322}

.

\sqrt{242}

.

\sqrt{152}

.

\sqrt{216}

.

Câu 5 (1đ):

Khảo sát thời gian tự học bài ở nhà của học sinh khối 9 ở trường X, ta thu được bảng sau:

Thời gian (phút)	Số học sinh
$\big[0 \, ; \, 30\big)$	$9$
$\big[30 \, ; \, 60\big)$	$10$
$\big[60 \, ; \, 90\big)$	$9$
$\big[90 \, ; \, 120\big)$	$15$
$\big[120 \, ; \, 150\big)$	$7$

Khoảng biến thiên của mẫu số liệu ghép nhóm trên là

120.

30.

90.

150.

Câu 6 (1đ):

Cho hàm số $y=\dfrac{x+m}{x-1}$ với $m$ là tham số. Số giá trị nguyên của $m$ thỏa mãn $\underset{\left[ 2;4 \right]}{\mathop{\min }}\,y=3$ là

2

.

8

.

1

.

3

.

Câu 7 (1đ):

Gọi $M$ và $m$ lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số $y=2\sin x$ trên đoạn $\Big[ -\dfrac{\pi }{6};\dfrac{5\pi }{6} \Big]$ . Tích $m.M$ bằng

-2

.

2

.

4

.

-\dfrac12

.

Câu 8 (1đ):

Một tác giả muốn xuất bản một cuốn sách Toán học. Biết phí xuất bản là $7$ triệu đồng và giá tiền in mỗi cuốn sách là $50$ nghìn đồng. Gọi $t \ge 1$ là số cuốn sách sẽ in và $f(t)$ (nghìn đồng) là chi phí trung bình của mỗi cuốn sách. Phương trình đường tiệm cận ngang của đồ thị hàm số $y = f(t)$ là

y = 50

.

y = 30

.

y = 45

.

y = 60

.

Câu 9 (1đ):

Trong mặt phẳng tọa độ $Oxy$ , gọi $(C )$ là đồ thị hàm số $y=\dfrac{x-1}{x-2}$ . Phương trình tiếp tuyến của $(C )$ tại giao điểm của đồ thị $(C )$ với trục hoành là

y=x-2

.

y=-x+2

.

y=x-1

.

y=-x+1

.

Câu 10 (1đ):

Trong không gian với hệ trục tọa độ $O x y z$ , cho tam giác $A B C$ có ba đỉnh $A(-1 ; 1 ;-3)$ , $B (4 ; 2 ; 1)$ , $C( 3 ; 0 ; 5)$ . Tọa độ trọng tâm $G$ của tam giác $A B C$ là

G (2 ; 1 ; 1).

G (3 ; 1 ; 1).

G (1 ; 3 ; 2).

G(-1 ; 2 ; 1).

Câu 11 (1đ):

Phỏng vấn một số học sinh khối 11 về thời gian (giờ) ngủ của một buổi tối, người ta thu được bảng số liệu sau:

Thời gian (giờ)	Số lượng
$[4;5)$	$6$
$[5;6)$	$12$
$[6;7)$	$13$
$[7;8)$	$10$
$[8;9)$	$3$

Khoảng tứ phân vị của bảng số liệu trên gần nhất với giá trị nào dưới đây?

1,79

.

1,78

.

1,97

.

1,87

.

Câu 12 (1đ):

Mỗi ngày bác Hương đều đi bộ để rèn luyện sức khỏe. Quãng đường đi bộ mỗi ngày (đơn vị: km) của bác Hương trong $20$ ngày được thống kê lại ở bảng sau:

Quãng đường (km)	Số ngày
$[ 2,7;3,0 )$	$3$
$[ 3,0;3,3 )$	$6$
$[ 3,3;3,6 )$	$5$
$[ 3,6;3,9 )$	$4$
$[ 3,9;4,2 )$	$2$

Phương sai của mẫu số liệu ghép nhóm là (làm tròn đến hàng phần trăm)

0,36

.

0,13

.

11,62

.

3,39

.

Câu 13 (1đ):

Chi phí nhiên liệu của một chiếc tàu chạy trên sông được chia làm hai phần. Phần thứ nhất không phụ thuộc vào vận tốc và bằng $480$ nghìn đồng mỗi giờ. Phần thứ hai tỉ lệ thuận với lập phương của vận tốc, khi $v=10$ km/h thì phần thứ hai bằng 30 nghìn đồng mỗi giờ.

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Khi vận tốc $v=10$ (km/h) thì chi phí nguyên liệu cho phần thứ nhất trên mỗi km đường sông là $48\,000$ đồng.
b) Hàm số xác định tổng chi phí nguyên liệu trên mỗi km đường sông với vận tốc $x$ km/h là $f(x)=\dfrac{480}{x}+0,03 x^{3}$ .
c) Khi vận tốc $v=30$ km/h thì tổng chi phí nguyên liệu trên mỗi km đường sông là $43\,000$ đồng.
d) Vận tốc của tàu để tổng chi phí nguyên liệu trên mỗi km đường sông nhỏ nhất là $v=20$ km/h.

Câu 14 (1đ):

Cho hàm số $y=\dfrac{-x^2+4x+3+m}{x-2}$ có đồ thị $(C)$ .

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Khi $m=0$ , tiệm cận đứng của đồ thị hàm số là $x=2$ .
b) Khi $m=0$ , tọa độ giao điểm tiệm cận đứng của $(C)$ với đường thẳng $x-y-1=0$ thuộc parabol $y=x^2$ .
c) Khi $m=0$ , lấy $M$ là điểm bất kì trên đồ thị $(C)$ , gọi $d_1$ là khoảng cách từ $M$ đến đường tiệm cận đứng, gọi $d_2$ là khoảng cách từ $M$ đến đường thẳng $y=-x+2$ . Tích $d_1.d_2=7$ .
d) Gọi $S$ là tập hợp các giá trị nguyên dương của $m$ để $(C)$ không có tiệm cận đứng. Số phần tử của $S$ là $1$ .

Câu 15 (1đ):

Trong không gian cho hình lập phương $ABCD.{A}'{B}'{C}'{D}'$ có độ dài cạnh là $a$ . Gọi $O$ là giao điểm của $BD$ và $AC$ .

loading...

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) $\overrightarrow{{A}'C}-\overrightarrow{{A}'A}=\overrightarrow{AB}+\overrightarrow{AD}$ .
b) $\overrightarrow{B{C}'}=\overrightarrow{{A}'A}+\overrightarrow{{B}'{C}'}$ .
c) $\overrightarrow{{C}'O}=\overrightarrow{{C}'{A}'}-\overrightarrow{O{A}'}$ .
d) $\overrightarrow{{A}'D}.\overrightarrow{{A}'B}=0$ .

Câu 16 (1đ):

Bảng sau đây cho biết chiều cao của các học sinh lớp $12A$ và lớp $12B$ .

Chiều cao (cm)	Số học sinh của lớp 12A	Số học sinh của lớp 12B
$[145;150)$	$1$	$0$
$[150;155)$	$0$	$0$
$[155;160)$	$10$	$15$
$[160;165)$	$12$	$9$
$[165;170)$	$12$	$10$
$[170;175)$	$5$	$8$

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) So sánh hai khoảng biến thiên của hai mẫu số liệu trên, ta thấy mẫu số liệu về chiều cao của lớp $12A$ phân tán hơn lớp $12B$ .
b) Tứ phân vị thứ nhất của mẫu số liệu ghép nhóm về chiều cao của học sinh lớp $12A$ là $159,5$ .
c) Khoảng tứ phân vị của mẫu số liệu ghép nhóm về chiều cao của học sinh lớp $12B$ là $9,5$ .
d) So sánh hai khoảng tứ phân vị của hai mẫu số liệu ghép nhóm, ta thấy mẫu số liệu ghép nhóm về chiều cao của học sinh lớp $12A$ phân tán hơn của lớp $12B$ .

Câu 17 (1đ):

Bảng thống kê cân nặng của $50$ quả xoài được lựa chọn ngẫu nhiên sau khi thu hoạch ở nông trường như sau:

Cân nặng (g)	Số quả xoài
$[250;290)$	$2$
$[290;330)$	$12$
$[330;370)$	$19$
$[370;410)$	$12$
$[410;450)$	$5$

Tìm khoảng tứ phân vị của mẫu số liệu ghép nhóm trên.

Trả lời: .

Câu 18 (1đ):

Cho hàm số $y=f(x)$ liên tục trên $\mathbb{R}$ và có đồ thị như hình vẽ:

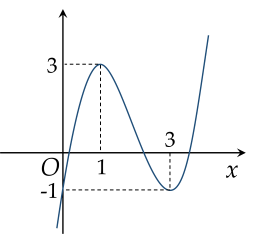
loading...

Có bao nhiêu giá trị nguyên của tham số $m$ để phương trình $f(| x+m | )=m$ có đúng $6$ nghiệm phân biệt?

Trả lời:

Câu 19 (1đ):

Cho một tấm nhôm hình vuông có cạnh $24$ cm. Người ta cắt ở bốn góc của tấm nhôm đó bốn hình vuông bằng nhau, mỗi hình vuông có cạnh bằng $x$ (cm), rồi gấp tấm nhôm lại như hình vẽ dưới đây để được một khối hộp chữ nhật không nắp.

loading...

Tìm $x$ (đơn vị cm) sao cho thể tích khối hộp lớn nhất.

Trả lời:

Câu 20 (1đ):

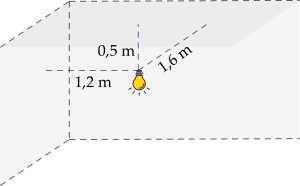
loading...

Hình vẽ trên minh hoạ một chiếc đèn được treo cách trần nhà là $0,5$ m, cách hai tường lần lượt là $1,2$ m và $1,6$ m. Hai bức tường vuông góc với nhau và cùng vuông góc với trần nhà. Người ta di chuyển chiếc đèn đó đến vị trí mới cách trần nhà là $0,4$ m, cách hai tường đều là $1,5$ m. Vị trí mới của bóng đèn cách vị trí ban đầu là bao nhiêu mét? (Làm tròn kết quả đến chữ số thập phân thứ hai)

Trả lời:

Câu 21 (1đ):

Gọi $M, \, N$ lần lượt là trung điểm của các cạnh $AC$ và $BD$ của tứ diện $ABCD$ . Gọi $I$ là trung điểm đoạn $MN$ và $P$ là điểm bất kì trong không gian. Tìm giá trị $k$ trong đẳng thức vectơ $\overrightarrow{P I}=k(\overrightarrow{P A}+\overrightarrow{P B}+\overrightarrow{P C}+\overrightarrow{PD})$ . (Ghi kết quả dưới dạng số thập phân)

Trả lời:

Câu 22 (1đ):

Một bể chứa $1\,000$ lít nước tinh khiết. Người ta bơm vào bể đó nước muối có nồng độ $15$ gam muối cho mỗi lít nước với tốc độ $20$ lít/phút. Biết rằng nồng độ muối trong bể sau $t$ phút (tính bằng tỉ số của khối lượng muối trong bể và thể tích nước trong bể, đơn vị: gam/lít) là một hàm số $f\left(t \right)$ , thời gian $t$ tính bằng phút. Phương trình tiệm cận ngang của đồ thị hàm số $y = f(t)$ là $y = a$ . Tính $a$ .

Trả lời:

Bài học cùng chủ đề

Đề kiểm tra học kì I (đề số 3) SVIP

Yêu cầu đăng nhập!

Bài học cùng chủ đề

Báo cáo học liệu

Mua học liệu

Mua học liệu:

Số dư ví của bạn: 0 coin - 0 Xu

Nếu mua học liệu này bạn sẽ bị trừ: 0 coin\Xu

Để nhận Coin\Xu, bạn có thể:

Chi tiết xem tại đây

Thông tin của bạn

Đề kiểm tra học kì I (đề số 3) SVIP

Yêu cầu đăng nhập!

Truy vết IP log

Báo lỗi câu hỏi

Các khóa học có thể bạn quan tâm

Yêu cầu VIP