Đề thi giữa học kì I toán 10 Kết nối tri thức cấu trúc mới

Câu 1 (1đ):

Trong các câu sau, có bao nhiêu câu là mệnh đề chứa biến và không phải mệnh đề?

i) " $2x+1$ là số lẻ, ( $x$ là số tự nhiên)".

ii) " $x+1=0$ ".

iii) " $x-2y>0$ ".

iv) " $(x+y)^2$ là số chính phương, ( $x,\,y$ là số tự nhiên khác $0$ )".

4

.

3

.

2

.

1

.

Câu 2 (1đ):

Mệnh đề phủ định của "14 là số nguyên tố" là

"14 không phải là số nguyên tố".

"14 chia hết cho 7".

"14 là số nguyên tố".

"14 chia hết cho 2".

Câu 3 (1đ):

Cho hai tập hợp $A$ và $B$ được minh họa bằng biểu đồ Ven như hình vẽ:

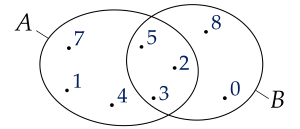
loading...

Khi đó tập hợp $C = A\cup B$ là

\left\{ 1;\,4;\,7 \right\}

.

\left\{ 0;\,1;\,2;\,3;\,4;\,5;\,7;\,8 \right\}

.

\left\{ 0;\,8 \right\}

.

\left\{ 2;\,3;\,5 \right\}

.

Câu 4 (1đ):

Cặp số $(x;y )=(-9;8)$ là một nghiệm của bất phương trình nào sau đây?

2x-y+1\le 0

.

x+3y-5<0

.

-x+y+5<0

.

2x+y-1>0

.

Câu 5 (1đ):

Hệ bất phương trình nào sau đây không là hệ bất phương trình bậc nhất hai ẩn?

\left\{ \begin{aligned} & x+y-6>0 \\ & x \ge 0 \\ & y\ge 0 \\ & 3x+y \le 6 \\ \end{aligned} \right.

.

\left\{ \begin{aligned} & x<0 \\ & x+y \le \dfrac32 \\ \end{aligned} \right.

.

\left\{ \begin{aligned} & -2x + y > 3^2 \\ & x + 4^2y \le 1 \\ \end{aligned} \right.

.

\left\{ \begin{aligned} & x \ge 1 \\ & 2x - xy\ge 0 \\ \end{aligned} \right.

.

Câu 6 (1đ):

Giá trị của biểu thức $P=\sin 30^\circ. \cos 60^\circ + \sin 60^\circ. \cos 30^\circ$ là

P=0

.

P=1

.

P=\sqrt{3}

.

P=-\sqrt{3}

.

Câu 7 (1đ):

Cho tam giác $ABC$ có $\widehat{B}=45^\circ$ , cạnh $AC=2\sqrt{2}$ cm. Bán kính $R$ của đường tròn ngoại tiếp tam giác $ABC$ bằng

4

cm.

3

cm.

2

cm.

1

cm.

Câu 8 (1đ):

Cho tam giác $ABC$ với $BC=7$ cm, $AC=9$ cm, $AB=4$ cm. Giá trị $\cos A$ bằng

\dfrac{1}{3}

.

\dfrac{1}{2}

.

\dfrac{2}{3}

.

-\dfrac{2}{3}

.

Câu 9 (1đ):

Cho hai tập hợp $A=\Big\{ x \in \mathbb{Z} \, \big| \, 2x^2-3x+1=0\Big\}, \, B=\Big\{ x \in \mathbb{N} \, \big| \, 3x+2<9 \Big\}$ . Khi đó $A \cap B$ là

\left\{ 2;5;7 \right\}

.

\Big\{ 0;1;2;\dfrac{1}{2} \Big\}

.

\left\{ 1 \right\}

.

\left\{ 0;2 \right\}

.

Câu 10 (1đ):

Miền tam giác $ABC$ kể cả ba cạnh (phần tô màu) trong hình vẽ là miền nghiệm của hệ bất phương trình nào trong bốn hệ bất phương trình dưới đây?

loading...

\left\{ \begin{aligned} & x\ge 0 \\ & 5x-4y\le 10 \\ & 4x+5y\le 10 \\ \end{aligned} \right.

.

\left\{ \begin{aligned} & x\ge 0 \\ & 4x-5y\le 10 \\ & 5x+4y\le 10 \\ \end{aligned} \right.

.

\left\{ \begin{aligned} & x>0 \\ & 5x-4y\le 10 \\ & 4x+5y\le 10 \\ \end{aligned} \right.

.

\left\{ \begin{aligned} & y\ge 0 \\ & 5x-4y\ge 10 \\ & 5x+4y\le 10 \\ \end{aligned} \right.

.

Câu 11 (1đ):

Cho $A = \cos (90^\circ-x). \sin (180^\circ-x)$ . Khẳng định nào sau đây đúng?

A=\cos^2 x

.

A=-\sin x\cos x

.

A=\sin^2 x

.

A=\sin x\cos x

.

Câu 12 (1đ):

Cho biết $\cos \alpha =-\dfrac23.$ Giá trị của $P=\dfrac{\cot \alpha +3\tan \alpha }{2\cot \alpha +\tan \alpha }$ bằng

-\dfrac{19}{13}.

\dfrac{25}{13}.

\dfrac{19}{13}.

-\dfrac{25}{13}.

Câu 13 (1đ):

Cho ba tập $A=\left[ -2;0 \right]$ , $B=\big\{ x\in \mathbb{R} \, \big| \, -1<x<0 \big\}$ , $C=\big\{ x\in \mathbb{R} \, \big| \, \left| x \right|<2 \big\}$ .

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) $B=\left(-1;0 \right)$ .
b) $C=\left(-\infty; -2\right) \cup \left(2 ;+\infty \right)$ .
c) $A \cap C=\left(-2;0 \right]$ .
d) $\left(A\cap C \right)\backslash B=\left(-2;-1 \right]$ .

Câu 14 (1đ):

Một công ty viễn thông tính phí $1$ $000$ đồng mỗi phút gọi nội mạng và $2$ $000$ đồng mỗi phút gọi ngoại mạng. Gọi $x$ và $y$ lần lượt là số phút gọi nội mạng, ngoại mạng của Bình trong một tháng và Bình muốn số tiền phải trả cho tổng đài luôn thấp hơn $100$ nghìn đồng.

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Số tiền Bình phải trả cho cuộc gọi nội mạng mỗi tháng là $x$ (nghìn đồng), số tiền phải trả cho cuộc gọi ngoại mạng mỗi tháng là $2y$ (nghìn đồng) và $x \in \mathbb{N}, \, y\in \mathbb{N}$ .
b) $x+2y<100$ .
c) Nếu $50$ và $20$ lần lượt là số phút gọi nội mạng, ngoại mạng của Bình trong một tháng thì số tiền phải trả cho tổng đài thấp hơn $100$ nghìn đồng.
d) Nếu $50$ và $25$ lần lượt là số phút gọi nội mạng, ngoại mạng trong một tháng thì số tiền phải trả cho tổng đài vượt quá mục tiêu của Bình.

Câu 15 (1đ):

Cho hệ bất phương trình $\left\{ \begin{aligned}& 3x+2y\ge 9 \\& x-2y\le 3 \\ & x+y\le 6 \\ & x\quad \ge 1 \\ \end{aligned} \right.$ (I).

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Miền nghiệm của hệ bất phương trình (I) là một miền tam giác.
b) $(3;2)$ là một nghiệm của hệ bất phương trình (I).
c) $x=1; \, y=3$ là nghiệm của hệ bất phương trình (I) thỏa mãn $F=3x-y$ đạt giá trị lớn nhất.
d) $x=1; \, y=5$ là nghiệm của hệ bất phương trình (I) thỏa mãn $F=3x-y$ đạt giá trị nhỏ nhất.

Câu 16 (1đ):

Cho $\cos \alpha =-\dfrac{3}{4}$ với $0^\circ <\alpha < 90^\circ$ .

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) $\sin^2 \alpha =\dfrac{7}{16}$ .
b) $\sin \alpha <0$ .
c) $\sin \alpha =-\dfrac{\sqrt{7}}{4}$ .
d) $\cot \alpha =-\dfrac{3\sqrt{7}}{7}$ .

Câu 17 (1đ):

Một lớp học có $25$ học sinh giỏi môn Toán, $23$ học sinh giỏi môn Lí, $14$ học sinh giỏi cả môn Toán và Lí và có $6$ học sinh không giỏi môn nào cả. Lớp học đó có bao nhiêu học sinh?

Trả lời:

Câu 18 (1đ):

Trong hệ tọa độ $Oxy$ , cho bất phương trình $2x+y\ge 2$ có miền nghiệm $D$ . Dựng hình vuông $ABCO$ có cạnh $a$ nằm trong góc phần tư thứ nhất, với $O(0;0)$ là gốc tọa độ. Biết rằng diện tích phần chung giữa miền nghiệm $D$ và hình vuông $ABCO$ bằng $2 \, 022$ . Tính $a$ (làm tròn kết quả đến hàng đơn vị).

Trả lời:

Câu 19 (1đ):

Một gia đình cần ít nhất $1 \, 200$ đơn vị protein và $800$ đơn vị lipit trong thức ăn mỗi ngày. Mỗi kilôgam thịt bò chứa $800$ đơn vị protein và $200$ đơn vị lipit. Mỗi kilôgam thịt lợn chứa $600$ đơn vị protein và $400$ đơn vị lipit. Biết rằng gia đình này chỉ mua nhiều nhất $2,0$ kg thịt bò và $1,5$ kg thịt lợn. Giá tiền $1$ kg thịt bò là $200$ nghìn đồng, $1$ kg thịt lợn là $100$ nghìn đồng. Gọi $x, \, y$ lần lượt là số kg thịt bò và thịt lợn mà gia đình đó cần mua để tổng số tiền họ phải trả là ít nhất mà vẫn đảm bảo lượng protein và lipit trong thức ăn. Tính $4x^2+y^2$ (làm tròn đến chữ số thập phân thứ hai)

Trả lời:

Câu 20 (1đ):

Hai tàu đánh cá cùng xuất phát từ bến $A$ và đi thẳng đều về hai vùng biển khác nhau, theo hai hướng tạo với nhau góc $120^\circ$ . Tàu thứ nhất đi với tốc độ $8$ hải lí một giờ và tàu thứ hai đi với tốc độ $10$ hải lí một giờ.

loading...

Sau mấy giờ thì khoảng cách giữa hai tàu là $60$ hải lí? (Làm tròn kết quả đến chữ số thập phân thứ nhất)

Trả lời:

Câu 21 (1đ):

Cho tam giác nhọn $ABC$ có $a=3, \, b=4$ và diện tích $S=3\sqrt{3}$ . Bán kính $R$ của đường tròn ngoại tiếp tam giác có dạng $R=\dfrac{\sqrt{m}}{n}$ , với $m, \, n\in \mathbb{N}, \, b\lt 5$ . Tính giá trị của biểu thức $T=m+n$ .

Trả lời:

Câu 22 (1đ):

Tìm giá trị nhỏ nhất của biết thức $F=x+y$ trên miền xác định bởi hệ $\left\{ \begin{aligned} & x \ge 0 \\ & 5x-4y \le 10 \\ & 4x+5y \le 10 \\ \end{aligned} \right.$ . (làm tròn kết quả đến chữ số thập phân thứ nhất)

Trả lời:

Bài học cùng chủ đề

Đề kiểm tra giữa học kì I (đề số 3) SVIP

Yêu cầu đăng nhập!

Bài học cùng chủ đề

Báo cáo học liệu

Mua học liệu

Mua học liệu:

Số dư ví của bạn: 0 coin - 0 Xu

Nếu mua học liệu này bạn sẽ bị trừ: 0 coin\Xu

Để nhận Coin\Xu, bạn có thể:

Chi tiết xem tại đây

Thông tin của bạn

Đề kiểm tra giữa học kì I (đề số 3) SVIP

Tải đề xuống bằng file Word

Yêu cầu đăng nhập!

Truy vết IP log

Báo lỗi câu hỏi

Các khóa học có thể bạn quan tâm

Yêu cầu VIP