Định lí côsin và định lí sin SVIP

1. ĐỊNH LÍ CÔSIN TRONG TAM GIÁC

Định lí côsin

Trong tam giác \(ABC\) với \(BC=a,CA=b,AB=c.\) Khi đó:

\(a^{^{ }2}=b^2+c^2-2bc\cos A,\)

\(b^{^{ }2}=c^2+a^2-2ca\cos B,\)

\(c^{^{ }2}=a^2+b^2-2ab\cos C\).

Hệ quả: 

​\(\cos A=\dfrac{b^2+c^2-a^2}{2bc}\);​

\(\cos B=\dfrac{c^2+a^2-b^2}{2ca}\);

\(\cos C=\dfrac{a^2+b^2-c^2}{2ab}\).

Ví dụ. Cho tam giác \(ABC\) có các cạnh \(AC=10\) cm, \(BC=16\) cm và góc \(C\) bằng \(110^\circ\). Tính cạnh \(AB\) và góc \(A\) của tam giác đó.

Giải

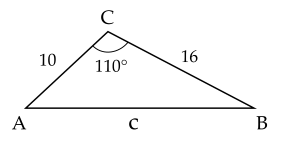
Theo định lí côsin ta có:

 \(AB^2=CA^2+CB^2-2CA.CB.\cos\widehat{C}\)

\(AB^2=16^2+10^2-2.16.10\)\(\cos110^\circ\)

\(AB^2\approx465,44\)

suy ra \(AB\approx\sqrt{465,44}\approx21,6\) (cm).

Theo hệ quả định lí côsin, ta có:

\(\cos A=\dfrac{AB^2+AC^2-BC^2}{2.AB.AC}\)

\(\cos A\approx\dfrac{10^2+\left(21,6\right)^2-16^2}{2.10.21,6}\approx0,72\)

suy ra \(A\approx\) \(43^\circ56'\).

2. ĐỊNH LÍ SIN TRONG TAM GIÁC

Định lí sin

Trong tam giác \(ABC\) có \(BC=a,CA=b,AB=c\) và bán kính đường tròn ngoại tiếp bằng \(R\). Khi đó:

\(\dfrac{a}{\sin A}=\dfrac{b}{\sin B}=\dfrac{c}{\sin C}=2R\).

Hệ quả

\(a=2R\sin A;\)       \(b=2R\sin B;\)      \(c=2R\sin C;\)

\(\sin A=\dfrac{a}{2R};\)         \(\sin B=\dfrac{b}{2R};\)        \(\sin C=\dfrac{c}{2R}.\)

Ví dụ. Cho tam giác \(ABC\) có \(AB=6\) cm, \(\widehat{B}=30^\circ,\widehat{C}=45^\circ\), tính độ dài cạnh \(AC\) và bán kính đường tròn ngoại tiếp tam giác \(ABC.\)

Giải

Áp dụng định lí sin trong tam giác \(ABC\) ta có:

\(\dfrac{AC}{\sin B}=\dfrac{AB}{\sin C}\Rightarrow AC=\dfrac{AB.\sin B}{\sin C}=\dfrac{6.\sin30^\circ}{\sin45^\circ}\approx4,24\) cm.

Ta lại có 

\(\dfrac{AB}{\sin C}=2R\Rightarrow R=\dfrac{AB}{2.\sin C}=\dfrac{6}{2.\sin45^\circ}\approx4,24\) cm.

3. CÁC CÔNG THỨC TÍNH DIỆN TÍCH TAM GIÁC

Trong tam giác \(ABC\), ta kí hiệu:

• \(A,B,C\) là các góc của tam giác tại các đỉnh tương ứng.
• \(a,b,c\) tương ứng là độ dài của các cạnh đối diện với đỉnh \(A,B,C\).
• \(h_a,h_b,h_c\) là độ dài các đường cao lần lượt tương ứng với các cạnh \(BC,CA,AB.\)
• \(p\) là nửa chu vi.
• \(S\) là diện tích.
• \(R,r\) tương ứng là bán kính đường tròn ngoại tiếp, nội tiếp tam giác.

\(1\)) \(S=\dfrac{1}{2}ah_a=\dfrac{1}{2}bh_b=\dfrac{1}{2}ch_c;\)

\(2\)) \(S=\dfrac{1}{2}bc\sin A=\dfrac{1}{2}ca\sin B=\dfrac{1}{2}ab\sin C;\)

\(3\)) \(S=\dfrac{abc}{4R};\)

\(4\)) \(S=pr;\)

\(5\)) \(S=\sqrt{p\left(p-a\right)\left(p-b\right)\left(p-c\right)}\) (công thức Heron)