Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:
CHÚC MỪNG
Bạn đã nhận được sao học tập

Chú ý:
Thành tích của bạn sẽ được cập nhật trên bảng xếp hạng sau 1 giờ!
Đồ thị và sự biến thiên của hàm số lượng giác SVIP
Tải đề xuống bằng file Word
Đây là bản xem thử, hãy nhấn Luyện tập ngay để bắt đầu luyện tập với OLM
Câu 1 (1đ):
Hàm số y=cosx đồng biến trên khoảng nào sau đây?
(0;π).
(−π;0).
(2−π;2π).
(2π;π).
Câu 2 (1đ):
Hàm số y=cosx nghịch biến trên khoảng nào dưới đây?
(−π;−2π).
(−2π;0).
(0;π).
(−2π;2π).
Câu 3 (1đ):
Hàm số y=sinx đồng biến trên khoảng nào dưới đây?
(π;2π).
(2π;π).
(23π;2π).
(2π;23π).
Câu 4 (1đ):
Hai hàm số nào sau đây tăng trên khoảng (0;2π)?
y=tanx và y=cotx.
y=cotx và y=sinx.
y=sinx và y=tanx.
y=sinx và y=cosx.
Câu 5 (1đ):
Xét hàm số y=sinx trên đoạn [−π;0]. Khẳng định nào sau đây đúng?
Hàm số nghịch biến trên các khoảng (−π;−2π) và (−2π;0).
Hàm số nghịch biến trên khoảng (−π;−2π); đồng biến trên khoảng (−2π;0).
Hàm số đồng biến trên các khoảng (−π;−2π) và (−2π;0).
Hàm số đồng biến trên khoảng (−π;−2π); nghịch biến trên khoảng (−2π;0).
Câu 6 (1đ):
Trên khoảng (−6π;−5π), hàm số nào sau đây luôn nhận giá trị dương?
y=tanx
y=cosx.
y=cotx.
y=sinx.
Câu 7 (1đ):
Xét hàm số y=cosx trên khoảng (5π;34π). Hàm số đồng biến trên khoảng có độ dài là
6π.
4π.
127π.
3π.
Câu 8 (1đ):
Hàm số nào dưới đây có đồ thị là đường cong như hình vẽ?
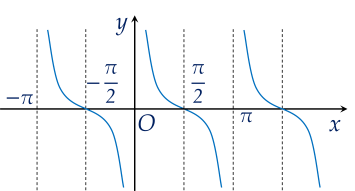
y=cotx.
y=tanx.
y=cosx.
y=sinx.
Câu 9 (1đ):
Đường cong hình bên dưới là đồ thị của hàm số nào trong bốn hàm số sau?
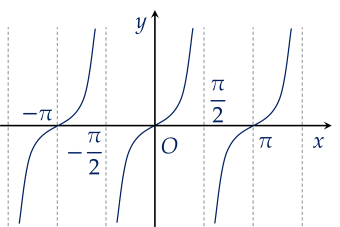
y=cosx.
y=cotx.
y=tanx.
y=sinx.
Câu 10 (1đ):
Cho các hàm số f(x)=sinx và g(x)=cosx.
(Nhấp vào ô màu vàng để chọn đúng / sai)| a) Hàm số f(x)=sinx đồng biến trên khoảng (−2π;2π). |
|
| b) Hàm số f(x) nghịch biến trên khoảng (43π;45π). |
|
| c) Hàm số g(x) nghịch biến trên khoảng (0;π). |
|
| d) Hàm số g(x) đồng biến trên khoảng (625π;313π). |
|
25%
Đúng rồi !

Hôm nay, bạn còn lượt làm bài tập miễn phí.
Hãy
đăng nhập
hoặc
đăng ký
và xác thực tài khoản để trải nghiệm học không giới hạn!
K
Khách
Bạn có thể đăng câu hỏi về bài học này ở đây
Chưa có câu hỏi thảo luận nào về bài giao này
OLMc◯2022
