Bài học cùng chủ đề
Kiến thức trọng tâm: Thống kê SVIP
1. CÁC KHÁI NIỆM
Mẫu số liệu | là tập hợp các dữ liệu thu thập được theo tiêu chí cho trước. |
Mẫu số liệu ghép nhóm | Gồm các nhóm với nửa khoảng $[a ; b)$, trong đó nửa khoảng $[a ; b)$ là tập hợp các giá trị $x$ của số liệu sao cho $x \ge a$ và $x < b$; Độ dài của nửa khoảng $[a ; b)$ là $b - a$. |
Tần số | Số lần xuất hiện của một giá trị trong mẫu dữ liệu thống kê được gọi là tần số của giá trị đó. Đối với một mẫu số liệu thống kê, tần số của một giá trị phản ánh số lần lặp đi lặp giá trị đó trong mẫu dữ liệu thống kê đã cho. |
Tần số tương đối | Tần số tương đối $f_i$ của giá trị $x_i$ là tỉ số giữa tần số $n_i$ của giá trị đó và số lượng $N$ các dữ liệu trong mẫu số liệu thống kê: $f_i = \dfrac{n_i}N$. Ta thường viết tần số tương đối dưới dạng phần trăm. Đối với một mẫu số liệu thống kê, tần số tương đối của một giá trị phản ánh giá trị đó chiếm bao nhiêu phần trăm trong tổng thể thống kê. |
Tần số tương đối ghép nhóm | Tần số tương đối ghép nhóm $f_i$ của giá trị $x_i$ là tỉ số giữa tần số $n_i$ của nhóm đó và số lượng $N$ các dữ liệu trong mẫu số liệu thống kê: $f_i = \dfrac{n_i}N$. |
2. BẢNG TẦN SỐ
a) Bảng tần số
Nhóm | $x_1$ | $x_2$ | ... | $x_i$ | Cộng |
Tần số ($n$) | $n_1$ | $n_2$ | ... | $n_i$ | $N = n_1 + n_2 + ... + n_i$ |
Trong đó, tần số của mỗi giá trị $x_1; \, x_2; \, …; \, x_i$ kí hiệu lần lượt là $n_1; \, n_2 ; \, ...;\, n_i$.
b) Bảng tần số tương đối
Nhóm | $x_1$ | $x_2$ | ... | $x_i$ | Cộng |
Tần số tương đối ($\%$) | $f_1$ | $f_2$ | ... | $f_i$ | $100$ |
Trong đó, $f_i$ của nhóm $i$ là tỉ số giữa tần số $n_i$ của giá trị đó và số lượng $N$ các dữ liệu trong mẫu số liệu thống kê: $f_i = \dfrac{n_i}N$.
c) Bảng tần số ghép nhóm
Nhóm | $[a_1 ; a_2)$ | $[a_2 ; a_3)$ | ... | $[a_{i-1} ; a_i)$ | Cộng |
Tần số ghép nhóm | $n_1$ | $n_2$ | ... | $n_i$ | $N =n_1 + n_2 + ... + n_i$ |
Trong đó, tần số của nhóm 1, nhóm 2, …, nhóm $i$ kí hiệu lần lượt là $n_1; \, n_2 ; \, ...;\, n_i$.
d) Bảng tần số tương đối ghép nhóm
Nhóm | $[a_1 ; a_2)$ | $[a_2 ; a_3)$ | ... | $[a_{i-1} ; a_i)$ | Cộng |
Tần số tương đối ghép nhóm ($\%$) | $f_1$ | $f_2$ | ... | $f_i$ | $100$ |
Trong đó, $f_i$ của nhóm $i$ là tỉ số giữa tần số $n_i$ của nhóm đó và số lượng $N$ các dữ liệu trong mẫu số liệu thống kê: $f_i = \dfrac{n_i}N$.
Chú ý: Bảng tần số ghép nhóm ở dạng bảng dọc được lập bằng cách tương tự .
3. BIỂU ĐỒ TẦN SỐ
a) Biểu đồ tần số
+ Trong biểu đồ tần số dạng cột, mỗi cột tương ứng với một giá trị, chiều cao của cột tương ứng tần số giá trị.
+ Trong biểu đồ tần số dạng đoạn thẳng, đường gấp khúc đi từ trái qua phải nối các điểm có hoành độ là giá trị số liệu và tung độ là tần số của giá trị đó.
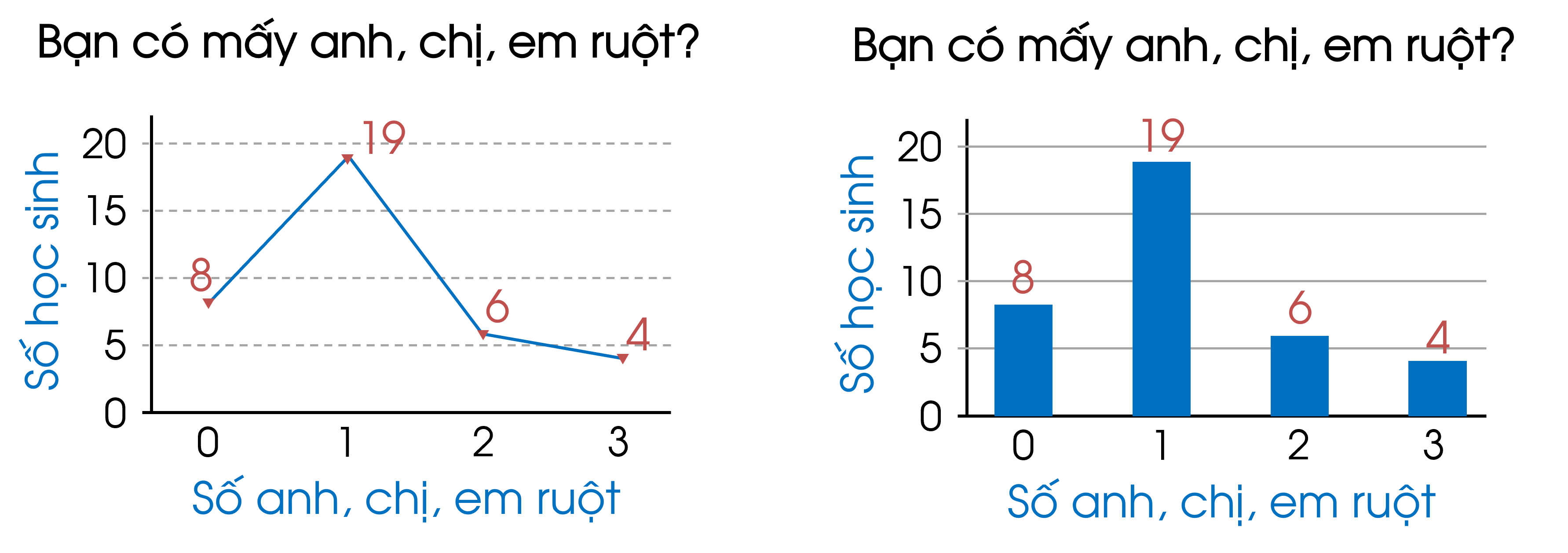
+ Người ta thường vẽ biểu đồ tần số ở dạng biểu đồ cột hoặc biểu đồ đoạn thẳng và có thể thực hiện các bước như sau:
⚡Bước 1: Lập bảng tần số của mẫu số liệu thống kê đó.
⚡Bước 2: Vẽ biểu đồ cột hoặc biểu đồ đoạn thẳng biểu diễn số liệu thống kê trong bảng tần số nhận được ở bước 1.
b) Biểu đồ tần số ghép nhóm
+ Trong biểu đồ hình quạt tròn, hình quạt tròn biểu thị tần số tương đối $a\%$ có số đo cung tương ứng là $a\% . 360^\circ = 3,6a^\circ$.
+ Trong biểu đồ cột, độ cao của mỗi cột tương ứng với tần số tương đối của từng giá trị.
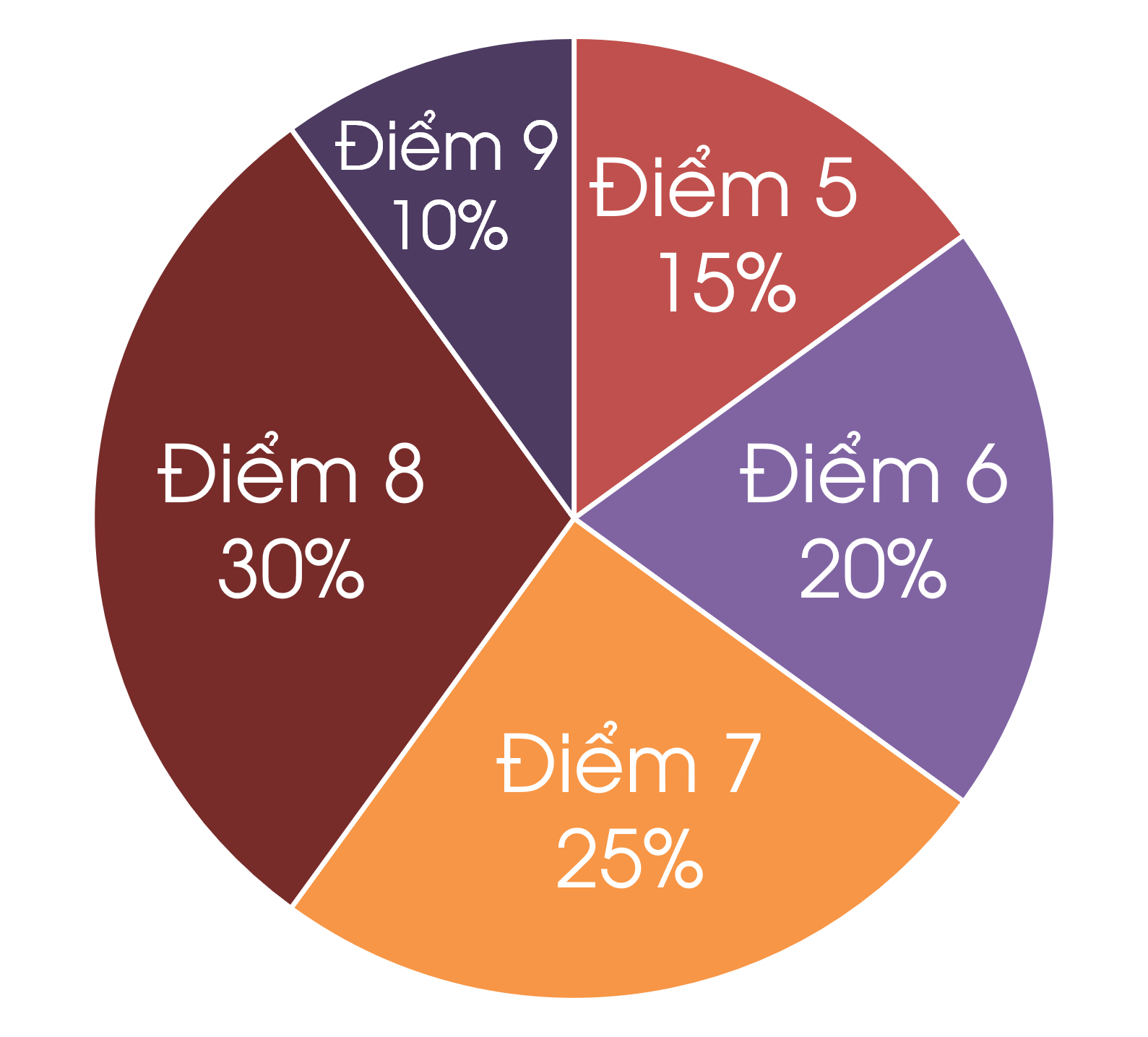
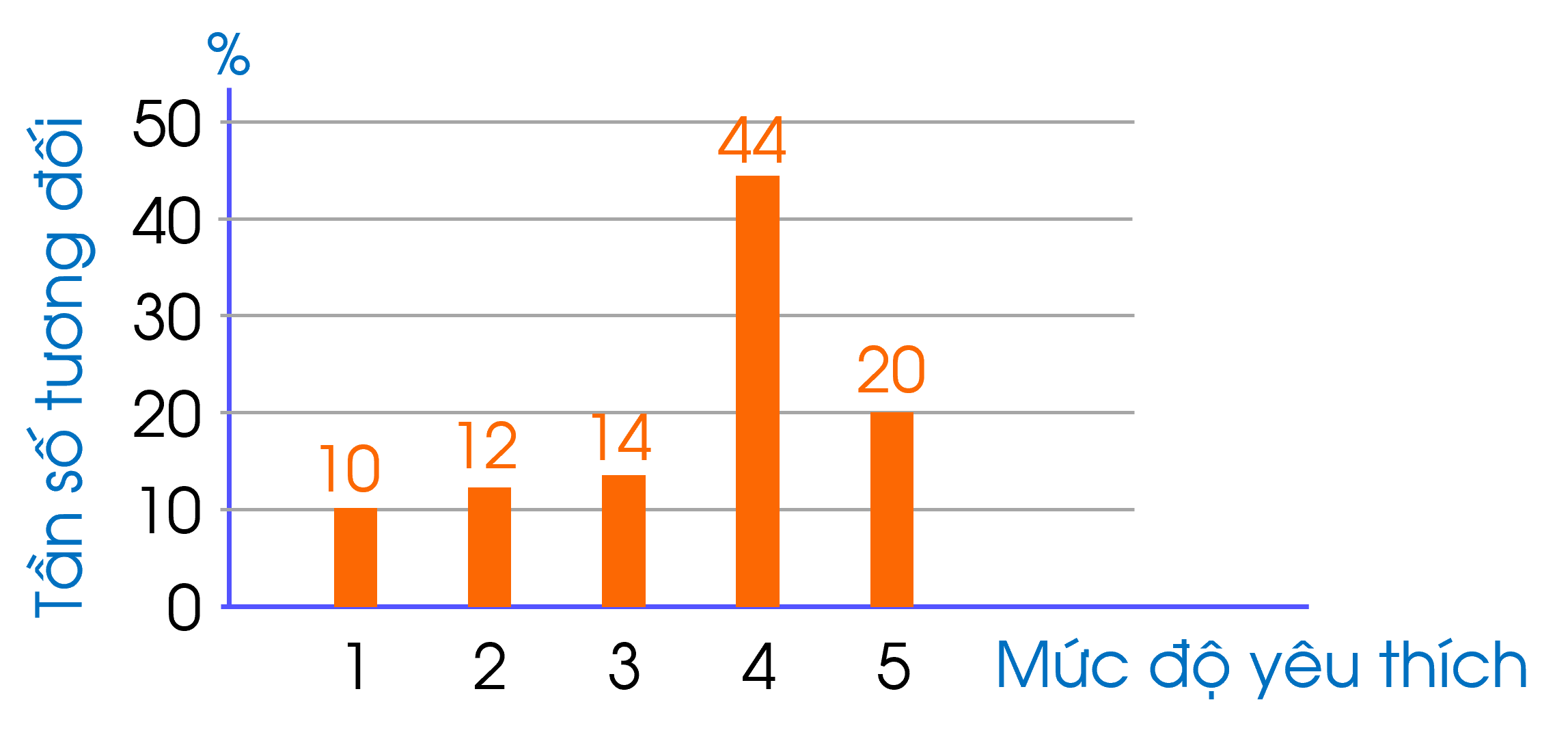
+ Để lập bảng tần số tương đối ở dạng biểu đồ cột hoặc quạt tròn của mẫu dữ liệu thống kê, ta có thể thực hiện các bước sau:
⚡Bước 1: Lập bảng tần số tương đối của mẫu số liệu thống kê đó.
⚡Bước 2: Vẽ biểu đồ cột/quạt tròn biểu diễn số liệu thống kê trong bảng tần tương đối số nhận được ở bước 1.
c) Biểu đồ tần số tương đối ghép nhóm
+ Biểu đồ tần số tương đối ghép nhóm có dạng cột kề nhau, mỗi cột tương ứng với một nhóm. Cột biểu diễn nhóm $[a_1 ; a_2)$ có đầu mút trái là $a_1$, đầu mút phải là $a_2$ và có chiều cao tuơng ứng với tần số tương ứng của nhóm.
+ Biểu đồ tần số tương đối ghép nhóm dạng đọan thẳng là đường gấp khúc đi từ trái qua phải, nối các điểm trên mặt phẳng, mỗi điểm có hoành độ là giá trị đại diện của nhóm số liệu và tung độ tương ứng với tần số tương đối của nhóm số liệu đó.
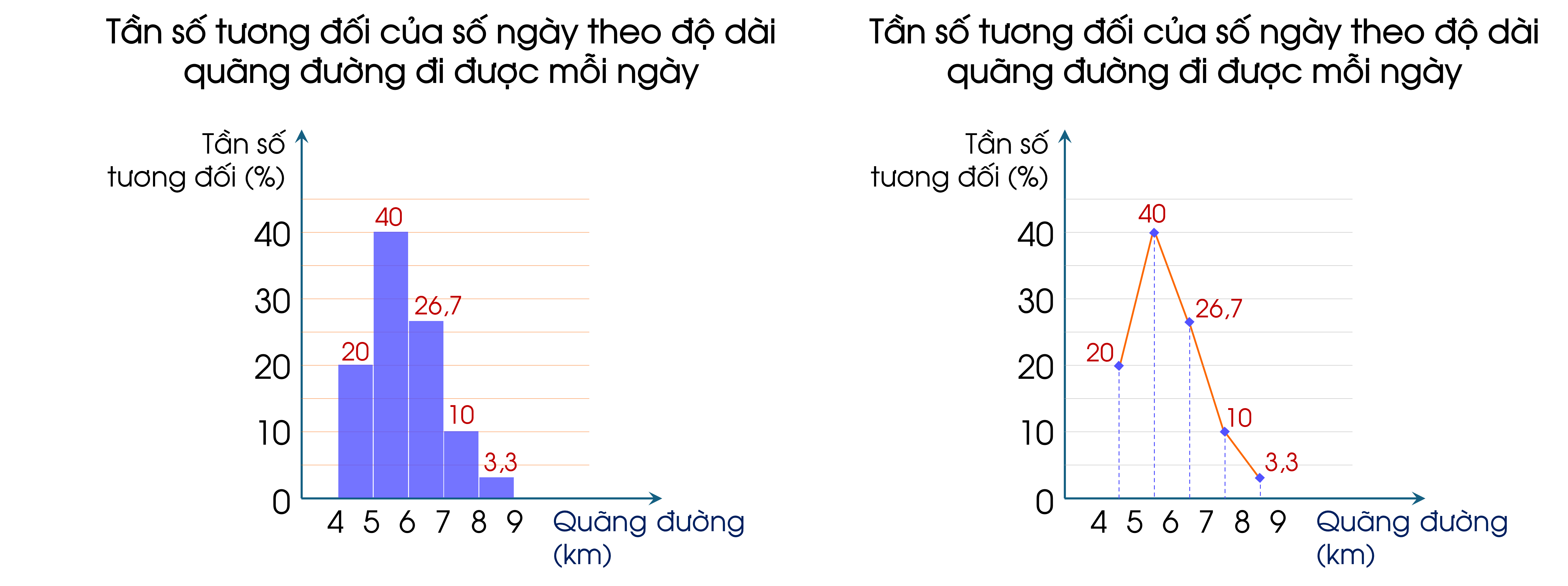
+ Để vẽ biểu đồ tần số tương đối ghép nhóm ở dạng biểu đồ cột hoặc đoạn thẳng của mẫu số liệu ghép nhóm, ta có thể thực hiện các bước sau:
⚡Bước 1: Lập bảng tần số tương đối ghép nhóm của mẫu số liệu ghép nhóm đã cho.
⚡Bước 2: Vẽ biểu đồ cột/đoạn thẳng biểu diễn số liệu thống kê trong bảng tần tương đối ghép nhóm nhận được ở bước 1.
Bài 1. Tỉ lệ học sinh bình chọn cho danh hiệu cầu thủ xuất sắc nhất trong giải bóng đá của trường được cho trong bảng sau:
Cầu thủ | Tuấn | Trường | An | Linh |
Tỉ lệ học sinh bình chọn | $30\%$ | $25\%$ | $10\%$ | $35\%$ |
Biết rằng có $500$ học sinh tham gia bình chọn. Lập bảng tần số học sinh bình chọn cho danh hiệu cầu thủ xuất sắc nhất trong giải bóng đá của trường.
Lời giải
Số học sinh bình chọn cho Tuấn là $\dfrac{500. 30\%}{100\%}=150$ (học sinh)
Số học sinh bình chọn cho Trường là $\dfrac{500.25\%}{100\%}=125$ (học sinh)
Số học sinh bình chọn cho An là $\dfrac{500.10\%}{100\%}=50$ (học sinh)
Số học sinh bình chọn cho Linh là $\dfrac{500.35\%}{100\%}=175$ (học sinh)
Ta có bảng tần số
Cầu thủ | Tuấn | Trường | An | Linh |
Số học sinh bình chọn | $150$ | $125$ | $50$ | $175$ |
Câu hỏi:
@204415716715@
Bài 2. Một cửa hàng tạp hóa thống kê số tiền lãi (đơn vị: nghìn đồng) trong $60$ ngày. Số liệu được ghi lại trong biểu đồ tần số ghép nhóm sau:
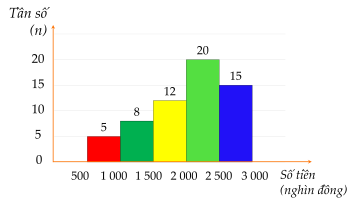
1) Tính tần số tương đối của mỗi nhóm?
2) Lập bảng tần số tương đối ghép nhóm cho bảng thống kê trên.
Lời giải
1) Tần số tương đối của mỗi nhóm là:
$f_1=\dfrac{5.100}{60}\%=8,3\%$;
$f_2=\dfrac{8.100}{60}\%=13,4\%$;
$f_3=\dfrac{12.100}{60}\%=20\%$;
$f_4=\dfrac{20.100}{60}\%=33,3\%$;
$f_5=\dfrac{15.100}{60}\%=25\%$.
2) Bảng tần số tương đối ghép nhóm của mẫu số liệu đã cho là:
Số tiền (nghìn đồng) | $[500;1\,000 )$ | $[ 1\,000;1\,500)$ | $[1\,500;2\,000)$ | $[2\,000;2\,500)$ | $[2\,500;3\,000)$ |
Tần số tương đối | $8,3\%$ | $13,4\%$ | $20\%$ | $33,3\%$ | $25\%$ |
Câu hỏi:
@204415688149@