Phương trình đường tròn. Phương trình tiếp tuyến của đường tròn SVIP

1. PHƯƠNG TRÌNH ĐƯỜNG TRÒN

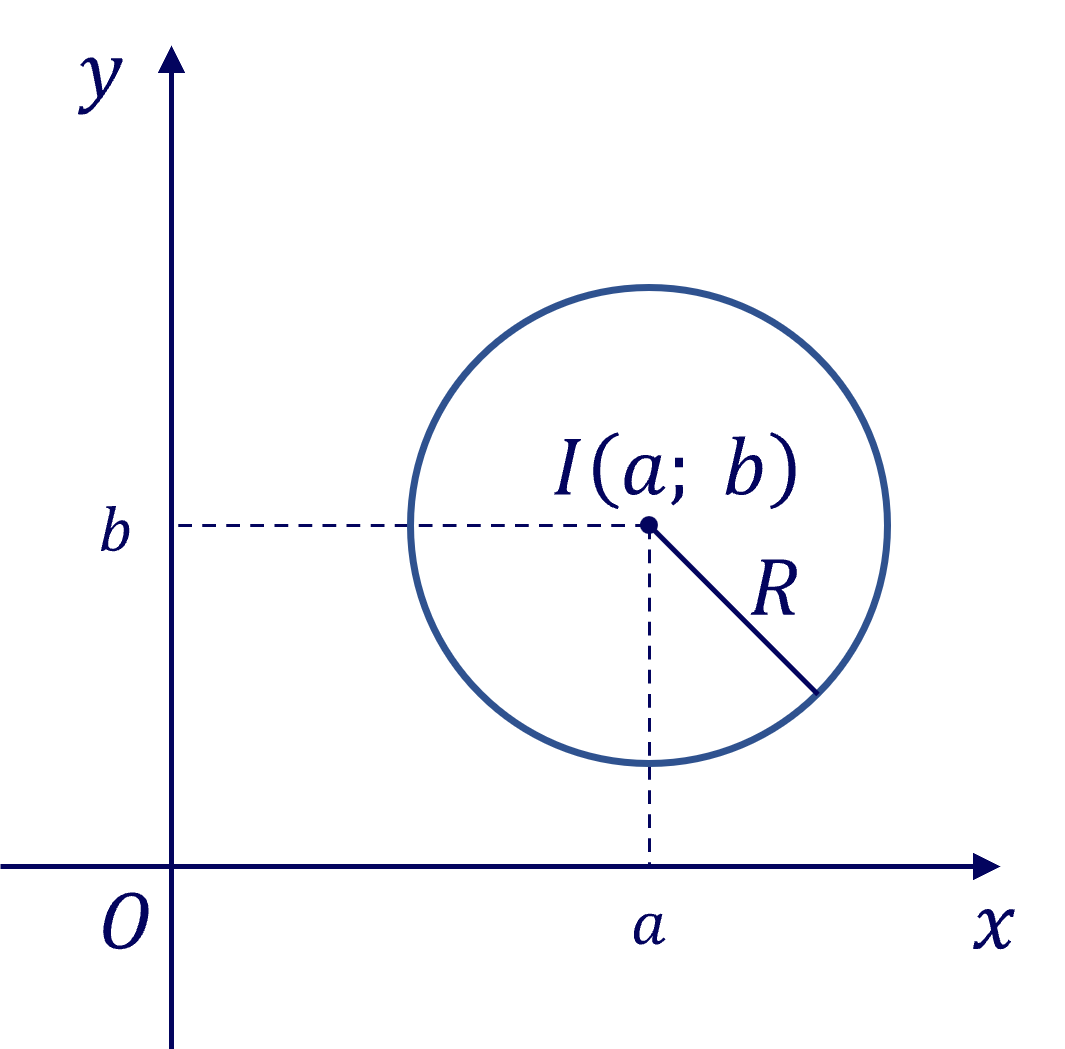
Phương trình của đường tròn \(\left(C\right)\) có tâm \(I\left(a;b\right)\), bán kính \(R\) là 

\(\left(x-a\right)^2+\left(y-b\right)^2=R^2\).

Với các hằng số \(a,b,c\) thỏa mãn \(a^2+b^2-c>0\), phương trình 

\(x^2+y^2-2ax-2by+c=0\)

là phương trình của một đường tròn có tâm \(I\left(a;b\right)\) và có bán kính \(R=\sqrt{a^2+b^2-c}\).

Ví dụ 1: Tìm tâm và bán kính của đường tròn trong mỗi trường hợp sau:

a) Đường tròn có phương trình \(\left(x+2\right)^2+\left(y-3\right)^2=25\);

b) Đường tròn có phương trình \(x^2+4x+y^2-6y-12=0\).

Giải

a) Ta có \(\left(x+2\right)^2+\left(y-3\right)^2=25\Leftrightarrow\left[x-\left(-2\right)\right]^2+\left(y-3\right)^2=5^2\).

Suy ra đường tròn có tâm \(I\left(-2;3\right)\) và bán kính \(R=5\).

b) Ta có \(x^2+4x+y^2-6y-12=0\Leftrightarrow x^2+y^2-2.\left(-2\right)x-2.3y-12=0\) và \(\left(-2\right)^2+3^2+12=25>0\)

suy ra đường tròn có tâm \(I\left(-2;3\right)\) và bán kính \(R=\sqrt{25}=5\).

Ví dụ 2: Viết phương trình đường tròn trong mỗi trường hợp sau: 

a) Có tâm \(I\left(-2;3\right)\) và đi qua \(A\left(2;0\right)\); 

b) Có tâm \(I\left(1;-2\right)\) và tiếp xúc với đường thẳng \(\Delta:3x-4y+14=0\). 

Giải

a) Vì đường tròn có tâm \(I\) và đi qua \(A\) nên có bán kính là 

\(R=IA=\left|\overrightarrow{IA}\right|=\sqrt{\left(2+2\right)^2+\left(0-3\right)^2}=5\). 

Vậy phương trình đường tròn là 

\(\left[x-\left(-2\right)\right]^2+\left(y-3\right)^2=5^2\Leftrightarrow\left(x+2\right)^2+\left(y-3\right)^2=25\).

b) Vì đường tròn có tâm \(I\) và tiếp xúc với đường thẳng \(\Delta\) nên bán kính \(R\) của đường tròn bằng khoảng cách từ điểm \(I\) đến đường thẳng \(\Delta\).

\(R=d\left(I,\Delta\right)=\dfrac{\left|3.1-4\left(-2\right)+14\right|}{\sqrt{3^2+4^2}}=5\).

Vậy phương trình đường tròn là 

\(\left(x-1\right)^2+\left[y-\left(-2\right)\right]^2=5^2\Leftrightarrow\left(x-1\right)^2+\left(y+2\right)^2=25\).

Ví dụ 3: Viết phương trình đường tròn \(\left(C\right)\) đi qua ba điểm \(A\left(2;6\right)\), \(B\left(-6;2\right)\), \(C\left(-1;-3\right)\). 

Giải

Cách 1: 

Phương trình đường tròn \(\left(C\right)\) có dạng \(x^2+y^2-2ax-2by+c=0\).

Vì \(A\left(2;6\right)\in\left(C\right)\) nên ta có \(2^2+6^2-2a.2-2b.6+c=0\Leftrightarrow4a+12b-c=0\) (1).

Tương tự, thay tọa độ các điểm \(B\), \(C\) vào phương trình \(\left(C\right)\) ta được hai phương trình 

\(12a-4b+c=-40\). (2) 

\(2a+6b+c=-10\). (3)

Cộng theo từng vế phương trình (1) với phương trình (2), phương trình (1) với phương trình (3), ta được hệ phương trình

\(\left\{{}\begin{matrix}16a+8b=0\\6a+18b=30\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-1\\b=2.\end{matrix}\right.\)

Suy ra \(c=4a+12b-40=-20\).

Vậy phương trình đường tròn \(\left(C\right)\) là \(x^2+y^2+2x-4y-20=0\).

Cách 2: 

Giả sử tâm của đường tròn là điểm \(I\left(a;b\right)\). Ta có \(IA=IB=IC\Leftrightarrow IA^2=IB^2=IC^2\).

Vì \(IA^2=IB^2\), \(IB^2=IC^2\)nên

\(\left\{{}\begin{matrix}\left(2-a\right)^2+\left(6-b\right)^2=\left(-6-a\right)^2+\left(2-b\right)^2\\\left(-6-a\right)^2+\left(2-b\right)^2=\left(-1-a\right)^2+\left(-3-b\right)^2\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}a^2-4a+4+b^2-12b+36=a^2+12a+36+b^2-4b+4\\a^2+12a+36+b^2-4b+4=a^2+2a+1+b^2+6b+9\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}-16a-8b=0\\10a-10b=-30\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-1\\b=2.\end{matrix}\right.\)

Bán kính đường tròn \(\left(C\right)\) là 

\(R=IA=\sqrt{\left[2-\left(-1\right)\right]^2+\left(6-2\right)^2}=5\).

Phương trình đường tròn \(\left(C\right)\) là

\(\left[x-\left(-1\right)\right]^2+\left(y-2\right)^2=5^2\Leftrightarrow\left(x+1\right)^2+\left(y-2\right)^2=25\).

Cách 3: 

Các đoạn thẳng \(AB\), \(AC\) tương ứng có các trung điểm là \(M\left(-2;4\right)\), \(N\left(\dfrac{1}{2};\dfrac{3}{2}\right)\).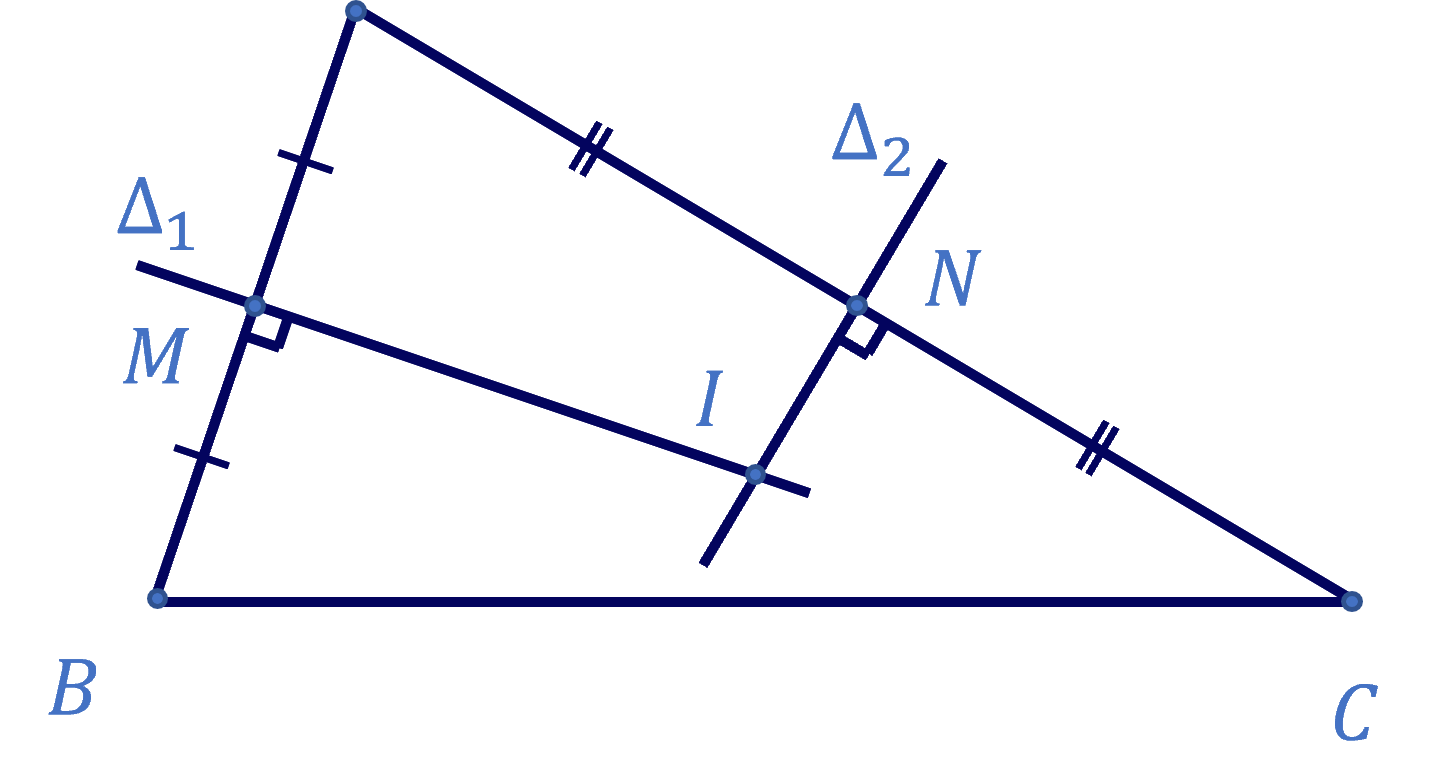

Đường trung trực \(\Delta_1\) của đoạn thẳng \(AB\) đi qua \(M\left(-2;4\right)\) và có vectơ pháp tuyến \(\overrightarrow{AB}=\left(-8;-4\right)\).

Vì \(\overrightarrow{AB}\left(-8;-4\right)\) cùng phương với \(\overrightarrow{n_1}\left(2;1\right)\) nên \(\Delta_1\) cũng nhận \(\overrightarrow{n_1}\left(2;1\right)\) là vectơ pháp tuyến. 

Do đó, phương trình của đường thẳng \(\Delta_1\) là 

\(2\left(x+2\right)+1\left(y-4\right)=0\) hay \(2x+y=0\).

Đường trung trực \(\Delta_2\) của đoạn thẳng \(AC\) đi qua \(N\left(\dfrac{1}{2};\dfrac{3}{2}\right)\) và có vectơ pháp tuyến \(\overrightarrow{AC}=\left(-3;-9\right)\).

Vì \(\overrightarrow{AC}\left(-3;-9\right)\) cùng phương với \(\overrightarrow{n_2}\left(1;3\right)\) nên \(\Delta_2\) cũng nhận \(\overrightarrow{n_2}\left(1;3\right)\) là vectơ pháp tuyến. 

Do đó, phương trình của đường thẳng \(\Delta_2\) là 

\(1\left(x-\dfrac{1}{2}\right)+3\left(y-\dfrac{3}{2}\right)=0\Leftrightarrow x+3y-5=0\).

Tâm \(I\) của đường tròn \(\left(C\right)\) là giao điểm của hai đường thẳng \(\Delta_1\) và \(\Delta_2\). 

Vậy tọa độ của \(I\) là nghiệm của hệ phương trình 

\(\left\{{}\begin{matrix}2x+y=0\\x+3y-5=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-1\\y=2.\end{matrix}\right.\)

Suy ra \(I\left(-1;2\right)\). Đường tròn \(\left(C\right)\) có bán kính là \(IA\).

\(IA=\left|\overrightarrow{IA}\right|=\sqrt{\left(-1-2\right)^2+\left(2-6\right)^2}=5\).

Vậy phương trình của \(\left(C\right)\) là \(\left(x+1\right)^2+\left(y-2\right)^2=25\). 

2. PHƯƠNG TRÌNH TIẾP TUYẾN CỦA ĐƯỜNG TRÒN

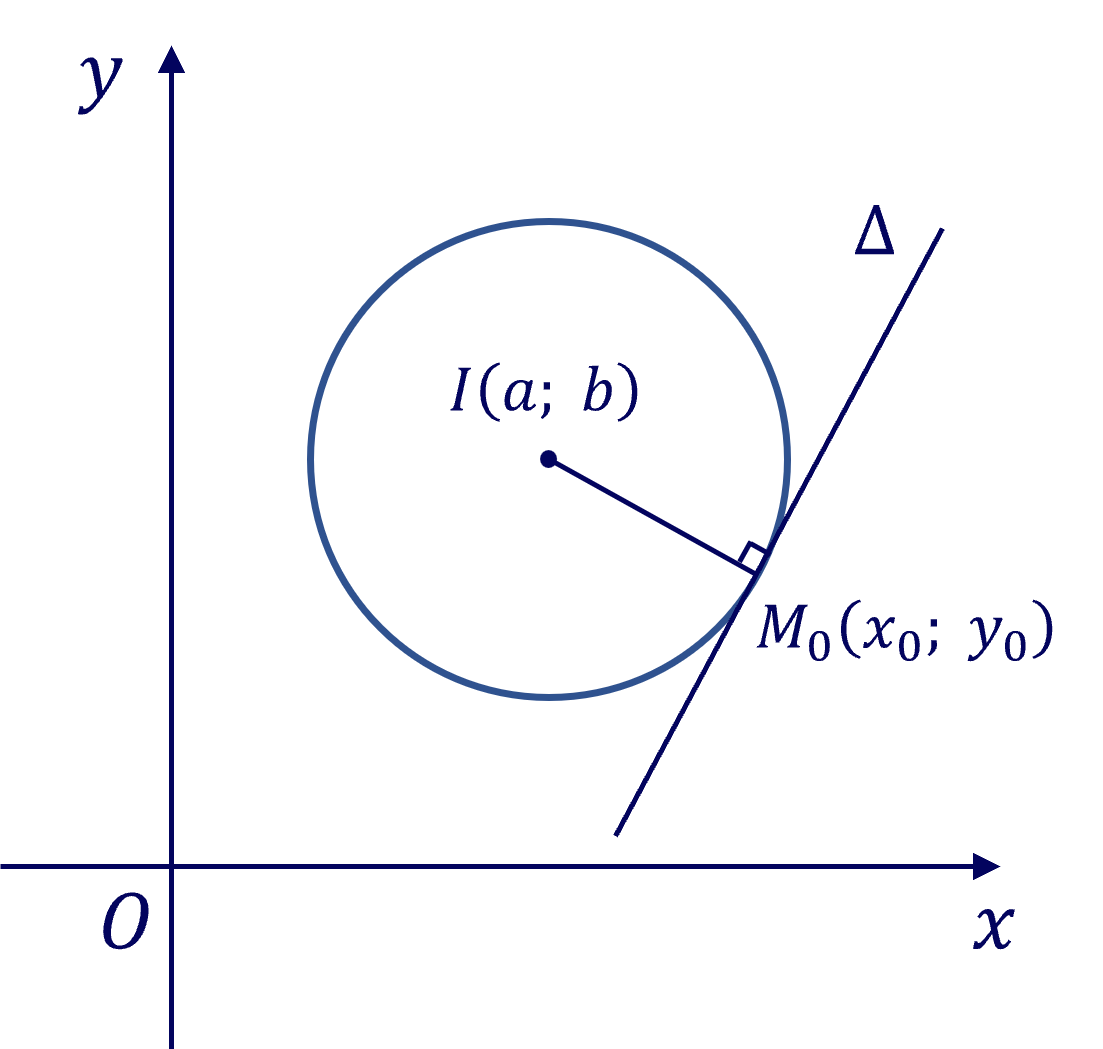
Cho đường tròn \(\left(C\right)\) có tâm \(I\left(a;b\right)\), bán kính \(R\).

Phương trình tiếp tuyến \(\Delta\) của \(\left(C\right)\) tại \(M_0\left(x_0;y_0\right)\) là

\(\left(a-x_0\right).\left(x-x_0\right)+\left(b-y_0\right).\left(y-y_0\right)=0\).

Ví dụ: Viết phương trình tiếp tuyến của đường tròn \(\left(C\right):x^2+y^2+2x-4y-20=0\). 

Giải

Đường tròn \(\left(C\right)\) có tâm \(I\left(-1;2\right)\), bán kính \(R=\sqrt{\left(-1\right)^2+2^2+20}=5\).

Tiếp tuyến \(\Delta\) của \(\left(C\right)\) vuông góc với đường thẳng \(IM\), do đó có vectơ pháp tuyến là

\(\overrightarrow{n_{\Delta}}=\overrightarrow{IM}=\left(3-\left(-1\right);5-2\right)=\left(4;3\right)\).

Đường thẳng \(\Delta\) có vectơ pháp tuyến \(\overrightarrow{n_{\Delta}}=\left(4;3\right)\) và đi qua điểm \(M\left(3;5\right)\) nên có phương trình

\(4\left(x-3\right)+3\left(y-5\right)=0\Leftrightarrow4x+3y-27=0\).