olm
Đăng nhập Đăng ký Trợ giúp

Bài học cùng chủ đề

Báo cáo học liệu
Mua học liệu
Mua học liệu:
  • Số dư ví của bạn: 0 coin - 0 Xu
  • Nếu mua học liệu này bạn sẽ bị trừ: 0 coin\Xu
Thông tin của bạn

Ôn tập và kiểm tra chương Hàm số và phương trình lượng giác SVIP

Tải ma trận In bài

Yêu cầu đăng nhập!

Bạn chưa đăng nhập. Hãy đăng nhập để làm bài thi tại đây!

Câu 1 (1đ):

Cho cos⁡α=12\cos \alpha =\dfrac{1}{2} và 3π2<α<2π\dfrac{3\pi }{2}<\alpha <2\pi . Khi đó sin⁡α\sin \alpha bằng

32\dfrac{\sqrt{3}}{2}.
−32-\dfrac{\sqrt{3}}{2}.
−22-\dfrac{\sqrt{2}}{2}.
22\dfrac{\sqrt{2}}{2}.
Câu 2 (1đ):

Cho 3π<α<10π33\pi <\alpha <\dfrac{10\pi }{3}, kết quả nào sau đây đúng?

cot⁡α<0\cot \alpha <0.
sin⁡α<0\sin \alpha <0.
tan⁡α<0\tan \alpha <0.
cos⁡α>0\cos \alpha >0.
Câu 3 (1đ):

Cho 2π<α<5π22\pi \lt \alpha \lt \dfrac{5\pi }{2}, kết quả nào sau đây đúng?

tan⁡α<0;cot⁡α>0\tan \alpha \lt 0;\cot \alpha >0.
tan⁡α<0;cot⁡α<0\tan \alpha \lt 0;\cot \alpha \lt 0.
tan⁡α>0;cot⁡α>0\tan \alpha >0;\cot \alpha >0.
tan⁡α>0;cot⁡α<0\tan \alpha >0;\cot \alpha \lt 0.
Câu 4 (1đ):

Giá trị lớn nhất của hàm số y=3sin⁡xy=3\sin x là

33.
−3-3.
22.
11.
Câu 5 (1đ):

Chu kì của hàm số y=cos⁡2xy=\cos 2x là

2π2\pi .
π\pi .
k2πk2\pi .
2π3\dfrac{2\pi }{3}.
Câu 6 (1đ):

Phương trình cot⁡x=cot⁡α\cot x=\cot \alpha có nghiệm là

x=k2πx=k2\pi , k∈Zk\in \mathbb{Z}.
x=kπx=k\pi , k∈Zk\in \mathbb{Z}.
x=α+k2πx=\alpha +k2\pi , k∈Zk\in \mathbb{Z}.
x=α+kπ, k∈Zx=\alpha +k\pi, \, k\in \mathbb{Z}.
Câu 7 (1đ):

Tập hợp tất cả các giá trị của tham số mm để phương trình cos⁡2x=m\cos 2x=m vô nghiệm là

(−∞;−1]∪[1;+∞)\left(-\infty ;-1 \right]\cup \left[ 1;+\infty \right).
(−1;1)\left(-1;1 \right).
(−∞;−1)∪(1;+∞)\left(-\infty ;-1 \right)\cup \left(1;+\infty \right).
[−1;1]\left[ -1;1 \right].
Câu 8 (1đ):

Cho cot⁡a=15\cot a=15, giá trị sin⁡2a\sin 2a bằng

17113\dfrac{17}{113}.
15113\dfrac{15}{113}.
13113\dfrac{13}{113}.
11113\dfrac{11}{113}.
Câu 9 (1đ):

Giá trị lớn nhất và giá trị nhỏ nhất của hàm số y=3sin⁡(x+3π4)−1y=3\sin \Big(x+\dfrac{3\pi }{4} \Big)-1 lần lượt là

4; −24; \, -2.
3; −33; \, -3.
2; −42; \, -4.
1; −11; \, -1.
Câu 10 (1đ):

Tập xác định của hàm số y=tan⁡x+cot⁡xy=\tan x+\cot x là

R\{kπ2 ∣ k∈Z}\mathbb{R}\backslash \left\{ k\dfrac{\pi }{2} \, \big| \, k\in \mathbb{Z} \right\}.
R\{kπ ∣ k∈Z}\mathbb{R}\backslash \left\{ k\pi \, \big| \, k\in \mathbb{Z} \right\}.
R\{π2+kπ ∣ k∈Z}\mathbb{R}\backslash \left\{ \dfrac{\pi }{2}+k\pi \, \big| \, k\in \mathbb{Z} \right\}.
R\mathbb{R}.
Câu 11 (1đ):

Phương trình 8sin⁡2(x2)cos⁡2(x2)−1=08\sin^2\Big(\dfrac{x}{2}\Big)\cos^2\Big(\dfrac{x}{2}\Big)-1=0 tương đương với phương trình nào sau đây?

sin⁡x=22\sin x=\dfrac{\sqrt{2}}{2}.
cos⁡x=22\cos x=\dfrac{\sqrt{2}}{2}.
sin⁡x=−22\sin x=-\dfrac{\sqrt{2}}{2}.
cos⁡2x=0\cos 2x=0.
Câu 12 (1đ):

Các nghiệm của phương trình cos⁡2x−sin⁡2x=0\cos^{2} x-\sin^{2} x=0 là

x=π4+kπ, (k∈Z)x=\dfrac{\pi }{4}+k\pi , \, (k \in \mathbb{Z})
x=π4+kπ2, (k∈Z)x=\dfrac{\pi }{4}+k\dfrac{\pi }{2}, \, (k \in \mathbb{Z}).
x=π2+kπ, (k∈Z)x=\dfrac{\pi }{2}+k\pi, \, (k \in \mathbb{Z}).
x=−π4+kπ, (k∈Z)x=-\dfrac{\pi }{4}+k\pi , \, (k \in \mathbb{Z}).
Câu 13 (1đ):

Cho tan⁡x=−2\tan x=-2 và biểu thức A1=5cot⁡x+4tan⁡x5cot⁡x−4tan⁡x, A2=2sin⁡x+cos⁡xcos⁡x−3sin⁡xA_1=\dfrac{5\cot x+4\tan x}{5\cot x-4\tan x}, \, A_2=\dfrac{2\sin x+\cos x}{\cos x-3\sin x}.

(Nhấp vào ô màu vàng để chọn đúng / sai)
a) cot⁡x=−12\cot x=-\dfrac12.
b) cos⁡x=0\cos x=0.
c) A1=−2111{{A}_{1}}=-\dfrac{21}{11}.
d) A2=37{{A}_{2}}=\dfrac{3}{7}.
Câu 14 (1đ):

Cho các hàm số f(x)=sin⁡xf(x)=\sin x và g(x)=cos⁡xg(x)=\cos x.

(Nhấp vào ô màu vàng để chọn đúng / sai)
a) Hàm số f(x)=sin⁡xf(x)=\sin x đồng biến trên khoảng (−π2;π2)\Big(-\dfrac{\pi }{2};\dfrac{\pi }{2} \Big).
b) Hàm số f(x)f(x) nghịch biến trên khoảng (3π4;5π4)\Big(\dfrac{3\pi }{4};\dfrac{5\pi }{4} \Big).
c) Hàm số g(x)g(x) nghịch biến trên khoảng (0;π)(0;\pi).
d) Hàm số g(x)g(x) đồng biến trên khoảng (25π6;13π3)\Big(\dfrac{25\pi }{6};\dfrac{13\pi }{3} \Big).
Câu 15 (1đ):

Cho phương trình lượng giác 2cos⁡x=32\cos x=\sqrt{3}.

(Nhấp vào ô màu vàng để chọn đúng / sai)
a) Phương trình có nghiệm x=±π3+k2π, (k∈Z)x=\pm \dfrac{\pi }{3}+k2\pi,\, (k\in \mathbb{Z}).
b) Trong đoạn [0;5π2]\Big[ 0;\dfrac{5\pi }{2} \Big] phương trình có 44 nghiệm.
c) Tổng các nghiệm của phương trình trong đoạn [0;5π2]\Big[ 0;\dfrac{5\pi }{2} \Big] bằng 25π6\dfrac{25\pi }{6}.
d) Trong đoạn [0;5π2]\Big[ 0;\dfrac{5\pi }{2} \Big] phương trình có nghiệm lớn nhất bằng 13π6\dfrac{13\pi }{6}.
Câu 16 (1đ):

Cho phương trình sin⁡2(2x+π4)=cos⁡2(x+π2)\sin^2\Big(2x+\dfrac{\pi }{4} \Big)=\cos^2\Big(x+\dfrac{\pi }{2} \Big) (*).

(Nhấp vào ô màu vàng để chọn đúng / sai)
a) Hạ bậc hai vế của (*), ta được phương trình: 1+cos⁡(4x+π2)2=1−cos⁡(2x+π)2\dfrac{1+\cos \Big(4x+\dfrac{\pi }{2} \Big)}{2}=\dfrac{1-\cos \Big(2x+\pi \Big)}{2}.
b) Ta có cos⁡(2x+π)=−cos⁡2x\cos \Big(2x+\pi \Big)=-\cos 2x.
c) Phương trình đã cho đưa về dạng: cos⁡(4x+π2)=cos⁡2x\cos \Big(4x+\dfrac{\pi }{2} \Big)=\cos 2x.
d) Nghiệm của phương trình (*) là x=−π4+kπx=-\dfrac{\pi }{4}+k\pi và x=π12+kπ3, (k∈Z)x=\dfrac{\pi }{12}+k\dfrac{\pi }{3}, \, (k \in \mathbb{Z}).
Câu 17 (1đ):

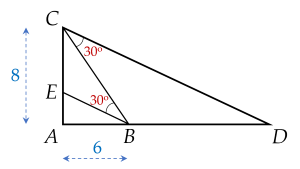
loading...

Cho tam giác ABCABC vuông tại AA có cạnh AB=6, AC=8AB=6, \, AC=8. Điểm EE thuộc đoạn ACAC sao cho CBE^=30∘\widehat{CBE}=30^\circ, điểm DD thuộc tia đối của tia BABA sao cho BCD^=30∘\widehat{BCD}=30^\circ. Tính độ dài đoạn ADAD. (làm tròn kết quả đến hàng phần mười)

Trả lời:

Câu 18 (1đ):

Có bao nhiêu giá trị nguyên của tham số mm để giá trị lớn nhất của hàm số y=msin⁡x+1cos⁡x+2y=\dfrac{m\sin x+1}{\cos x+2} nhỏ hơn 22?

Trả lời:

Câu 19 (1đ):

Trong môn cầu lông, khi phát cầu, người chơi cần đánh cầu qua khỏi lưới sang phía sân đối phương và không được để cho cầu rơi ngoài biên. Trong mặt phẳng toạ độ OxyOxy, chọn điểm có tọa độ (O;y0)\left(O;y_0\right) là điểm xuất phát thì phương trình quỹ đạo của cầu lông khi rời khỏi mặt vợt là: y=−g.x22.v02.cos⁡2α+tan⁡(α).x+y0y=\dfrac{-g.x^2}{2.v_{0}^{2}.\cos^{2}\alpha}+\tan (\alpha).x+y_0; trong đó: gg là gia tốc trọng trường (thường được chọn là 9,89,8 m/s2^{2}; α\alpha là góc phát cầu (so với phương ngang của mặt đất); v0{{v}_{0}} là vận tốc ban đầu của cầu; y0{{y}_{0}} là khoảng cách từ vị trí phát cầu đến mặt đất. Quỹ đạo chuyển động của quả cầu lông là một parabol như hình vẽ.

loading...

Một người chơi cầu lông đang đứng khoảng cách từ vị trí người này đến vị trí cầu rơi chạm đất (tầm bay xa) là 6,686,68 m. Người chơi đó đã phát cầu với góc tối đa khoảng bao nhiêu độ so với mặt đất? (biết cầu rời mặt vợt ở độ cao 0,70,7 m so với mặt đất và vận tốc xuất phát của cầu là 88 m/s, bỏ qua sức cản của gió và xem quỹ đạo của cầu luôn nằm trong mặt phẳng thẳng đứng, làm tròn kết quả tới hàng đơn vị).

Trả lời:

OLM©2022OLM \copyright 2022
Truy vết IP log
Báo lỗi câu hỏi
Bạn đã gặp lỗi gì ở câu hỏi này, hãy mô tả vào ô bên dưới. Với mỗi lỗi thông báo đúng, OLM sẽ tặng bạn 1-3 ngày VIP!
Bạn có thể báo lỗi bằng hình ảnh tại đây!!!
Các khóa học có thể bạn quan tâm
Tổng thanh toán: 0đ (Tiết kiệm: 0đ)
Tới giỏ hàng
Yêu cầu VIP