Phần tự luận (7 điểm) SVIP

Hướng dẫn giải:

Coi hệ gồm hai viên bi là một hệ kín.

Theo định luật bảo toàn động lượng ta có:

\(\overrightarrow{p_1}+\overrightarrow{p_2}=\overrightarrow{p}\) hay  \(m_1\overrightarrow{\text{v}}_1+m_2\overrightarrow{\text{v}}_2=\left(m_1+m_2\right)\overrightarrow{\text{v}}\)

a. Sau va chạm chúng dính vào nhau và chuyển động với vận tốc \(\text{v}\) = 3m/s theo hướng chuyển động ban đầu của viên bi 1.

Chọn chiều dương là chiều chuyển động của bi 1, bi 2 ban đầu.

Ta có: \(m_1\text{v}_1+m_2\text{v}_2=\left(m_1+m_2\right)\text{v}\)

\(\Rightarrow\text{v}_2=\dfrac{\left(m_1+m_2\right)\text{v}-m_1\text{v}_1}{m_2}=\dfrac{\left(0,5+0,3\right).3-0,5.4}{0,3}=1,33\) m/s

b. Sau va chạm chúng dính vào nhau và chuyển động động với vận tốc \(\text{v}\) = 3 m/s theo hướng vuông góc với hướng chuyển động ban đầu của viên bi 1.

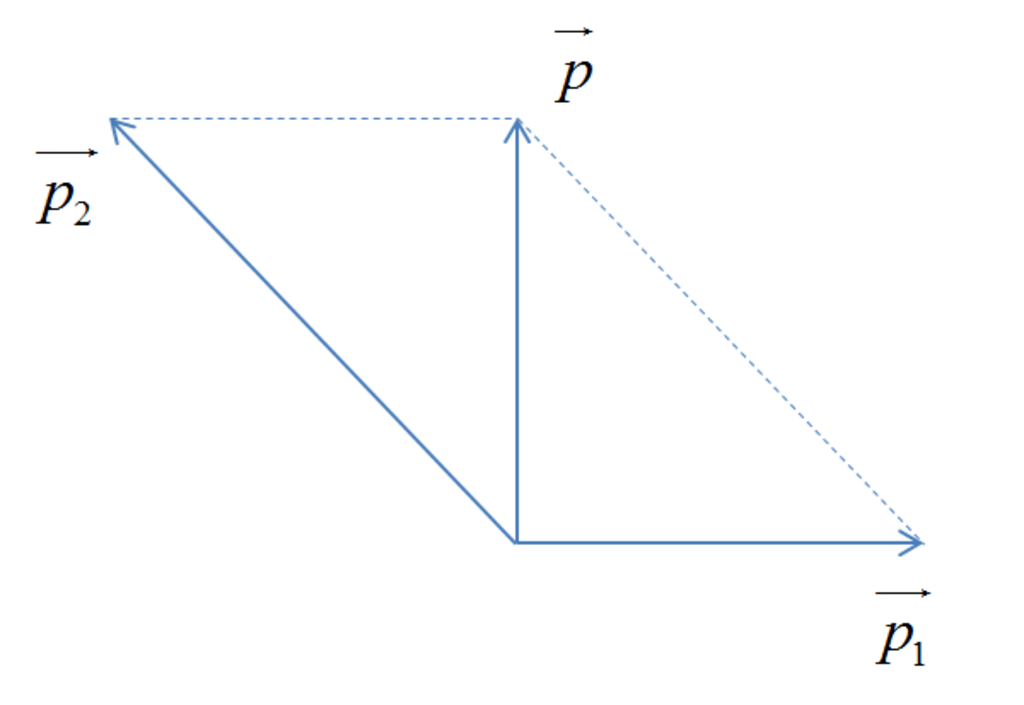
Từ hình vẽ ta suy ra: \(p_2=\sqrt{p^2+p_1^2}\)

\(p=\left(m_1+m_2\right)\text{v}=\left(0,5+0,3\right).3=2,4\) kg.m/s

\(p_1=m_1\text{v}_1=0,5.4=2\) kg.m/s

\(\Rightarrow p_2=3,12\) kg.m/s

\(\text{v}_2=\dfrac{p_2}{m_2}=\dfrac{3,12}{0,3}=10,4\) m/s

Hướng dẫn giải:

a. $r$ = 150 triệu km = 150.10⁹ m

$T_1$ = 365,25 ngày

\(\omega_1=\dfrac{2\pi}{T_1}=2.10^{-7}\) rad/s

\(v_1=\omega_1\left(r+R\right)=30001\) m/s

b. $R$ = 6400 km = 6400.10³ m

$T_2$ = 24 giờ

\(\omega_2=\dfrac{2\pi}{T_2}=7,27.10^{-5}\) rad/s

\(v_2=\omega_2R=465\) m/s

c. \(R=6400.\cos30^0=\dfrac{6400.\sqrt{3}}{2}\) m

\(T_3\) = 24 giờ

\(\omega_3=\dfrac{2\pi}{T_3}=7,27.10^{-5}\) rad/s

\(v_3=\omega_3R=402\) m/s

Hướng dẫn giải:

a. Độ dãn của lò xo khi hệ cân bằng:

Áp dụng định luật Hooke ở trạng thái cân bằng:

\(F_{đh}=P\Rightarrow k\cdot\Delta l=m\cdot g\)

\(\Delta l = \frac{m \cdot g}{k} = \frac{0,5 \cdot 9,8}{100} = \frac{4,9}{100} = 0,049 \textrm{ } \text{m} = 4,9 \textrm{ } \text{cm}\)

b. Lò xo có độ dãn cực đại là 10 cm → biên độ là phần dao động thêm so với vị trí cân bằng.

\(A = 10 \textrm{ } \text{cm} - 4,9 \textrm{ } \text{cm} = 5,1 \textrm{ } \text{cm}\)

c. Độ dãn tổng cộng:

\(\Delta l = 4,9 \textrm{ } \text{cm} + 6 \textrm{ } \text{cm} = 10,9 \textrm{ } \text{cm} = 0,109 \textrm{ } \text{m}\)

Lực kéo:

\(F = k \cdot \Delta l = 100 \cdot 0,109 = 10,9 \textrm{ } \text{N}\)