Sự tương giao của hai đồ thị chứa tham số liên quan đến định lí Viète (nâng cao) SVIP

Hướng dẫn giải:

a) Với $m=1$, đường thẳng $(d)$ có dạng $y=3 x-3+1$ hay $y=3 x-2$.

Khi đó, phương trình hoành độ giao điểm của đường thẳng $(d)$ và parabol $(P)$ là: $x^2=3x-2$

$x^2-3x+2=0$

Do $a+b+c=1+(-3)+2=0$ nên phương trình có hai nghiệm $x_1=1;$ $x_2=2$.

Với $x=x_1=1$ thì $y=1^2=1$

Với $x=x_2=2$ thì $y=2^2=4$

Vậy với $m=1$ thì toạ độ giao điểm của $(d)$ và $(P)$ là $(1;1); \,(2;4)$.

b) Phương trình hoành độ giao điểm của đường thẳng $(d)$ và parabol $(P)$ là: $x^2=3mx-3m+1$

$x^2-3mx+3m-1=0$ (*)

$\Delta = (-3m)^2-4.1. (3m-1)=9m^2-12m+4=(3m)^2-2.3m.2+2^2=(3m-2)^2$

Để $(d)$ cắt $(P)$ tại hai điểm phân biệt có hoành $x_1$; $x_2$ thì phương trình (*) phải có hai nghiệm phân biệt $x_1$; $x_2$

$\Delta >0$

$(3m-2)^2>0$

$3m-2\ne 0$

$3m\ne 2$

$m\ne \dfrac{2}{3}$ (**)

Khi đó, theo hệ thức Viète $\left\{ \begin{aligned}& x_1+x_2=3m\,\,\,(2) \\ &x_1.x_2=3m-1 \,\,\,(3) \\ \end{aligned} \right.$

Ta có $x_1+2 x_2=11$ $(4)$

Từ $(2)$; $(4)$ ta có hệ phương trình $\left\{ \begin{aligned} &x_1+x_2=3m \\ &x_1+2x_2=11 \\ & x_2=11-3m \\ &x_1+11-3m=3m \\ \end{aligned} \right.$

$\left\{ \begin{aligned} &x_2=11-3m \\ &x_1=3m+3m-11 \\ \end{aligned} \right.$

$\left\{ \begin{aligned} &x_1=6m-11 \\ &x_2=11-3m \\ \end{aligned} \right.$

Thế $x_1=6m-11; \, x_2=11-3m$ vào $(3)$ ta được:

$(6m-11).(11-3m)=3m-1$

$66m-18m^2-121+33m-3m+1=0$

$-18m^2+96m-120=0$

$18m^2-96m+120=0$

$3m^2-16m+20=0$ (5) 

$\Delta'=(-8)^2-3.20=64-60=4>0$.

Vì $\Delta' >0$ nên phương trình (5) có hai nghiệm phân biệt:

$m_1=\dfrac{-(-8)+\sqrt{4}}{3}=\dfrac{10}{3}$ thỏa mãn (**) 

$m_2=\dfrac{-(-8)-\sqrt{4}}{3}=2$ thỏa mãn (**)

Vậy $m \in \Big\{2 ; \dfrac{10}{3}\Big\}$ thoả mãn yêu cầu.

Hướng dẫn giải:

Phương trình hoành độ giao điểm của $(d)$ và $(P)$ là:

$x^2=-2x+m-1$

$x^2+2x-m+1=0$ (1) 

Để đường thẳng $d$ cắt parabol $(P)$ tại hai điểm phân biệt thì phương trình (1) có hai nghiệm phân biệt

Hay $\Delta'>0$

$1^2-1. (-m+1)>0$

$m>0$

Vậy $m>0$ thì đường thẳng $d$ cắt parabol $(P)$ tại hai điểm phân biệt $A( x_1;y_1), \, B( x_{2};y_2)$.

Khi đó ta có $y_1=x_{1}^{2}; \, y_2=x_{2}^{2}$

Theo định lí Viète ta có $x_1+x_2-2; \, x_1x_2=-m+1$.

Ta có $x_{1}^{2}+x_{2}^{2}=(x-1+x_2)^2-2x_1x_2=(-2)^2-2(-m+1)=2m+2$

Theo bài ra ta có $( y_1+y_2)^2=110-x_{1}^{2}-x_{2}^{2}$

$( x_{1}^{2}+x_{2}^{2} )^2=110-(x_{1}^{2}+x_{2}^{2})$

$(2m+2)^2=110-( 2m+2 )$

$2m^2+5m-52=0$

Ta có $\Delta = 5^2-4.1.(-52)=441$

Do $\Delta >0$ nên phương trình có hai nghiệm phân biệt $m_1=\dfrac{-5+21}{4}=4$ (thoả mãn điều kiện $m>0$)

$m_2=\dfrac{-5-21}{4}=\dfrac{-13}{2}$ (không thoả mãn điều kiện $m>0$)

Vậy $m=4$ thì đường thẳng $d$ cắt parabol $(P)$ tại hai điểm phân biệt $A( x_1;y_1)$ và $B( x_2;y_2)$ thỏa mãn yêu cầu.

Hướng dẫn giải:

a) Vẽ parabol $(P)$ là đồ thị của hàm số $y=x^2$

- Bảng giá trị của $y$ tương ứng với giá trị của $x$ như sau:

- Vẽ các điểm $A( -2;4 ), \, B( -1;1 ), \, O( 0;0 ), \, C( 1;1 ), \, D( 2;4 )$ thuộc đồ thị hàm số $y=x^2$ trong mặt phẳng $Oxy$.

- Vẽ đường parabol đi qua các điểm trên, ta nhận được đồ thị của hàm số $y=x^2$.

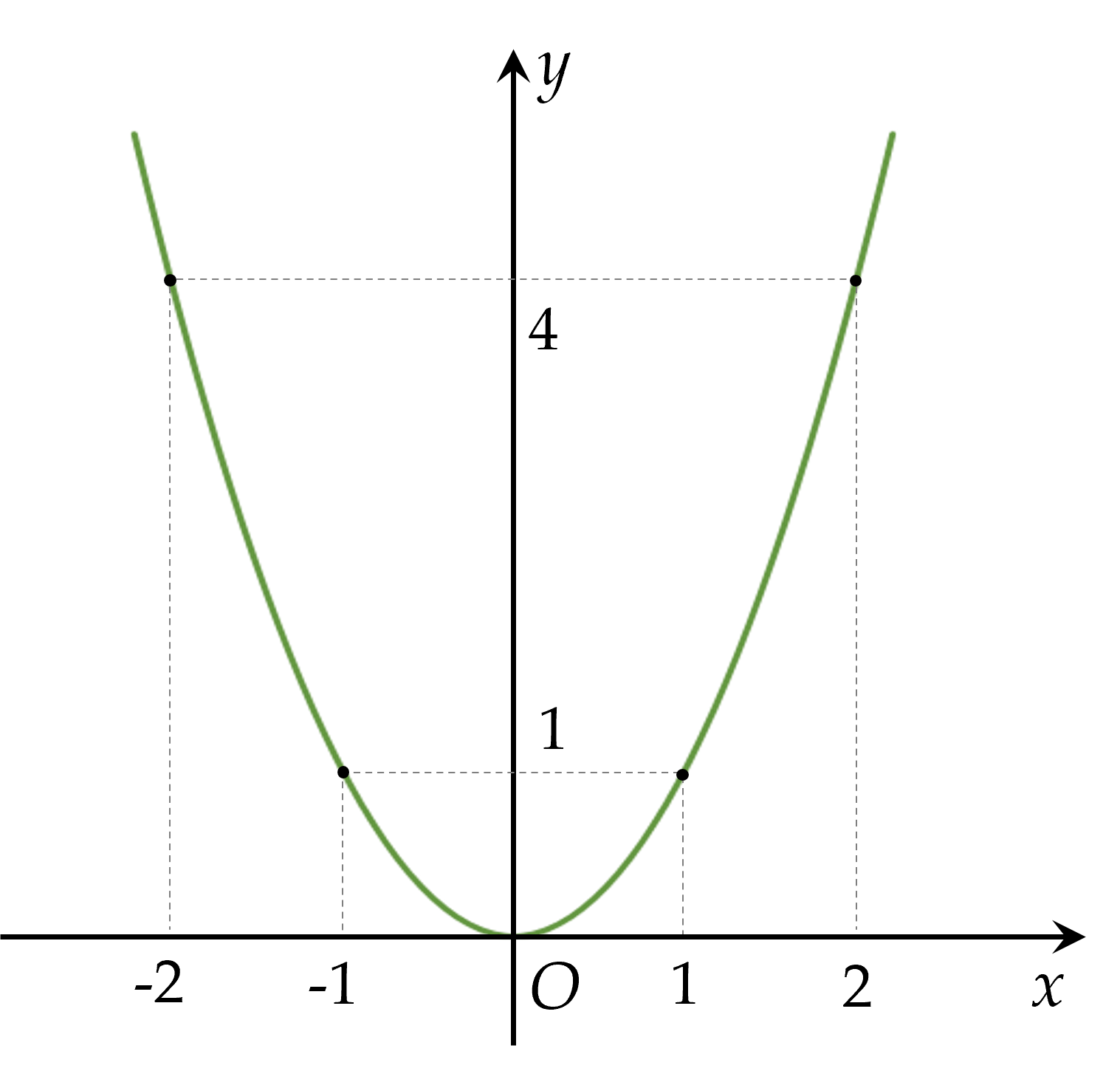
b) Phương trình hoành độ giao điểm của $(P)$ và $(d)$ là:

$x^2=2x+5m$

$x^2-2x-5m=0$.

Do $(d)$ cắt $(P)$ tại hai điểm phân biệt có hoành độ $x_1; \, x_2$ nên

$\Delta'>0$

$1^2+5m>0$

$m>-\dfrac{1}{5}$.

Khi đó, theo định lí Viète ta có: 

$\left\{ \begin{aligned} &x_1+x_2=-\dfrac{-2}{1}=2\,\,\,(1) \\ & x_1x_2=\dfrac{-5m}{1}=-5m\,\,\,(2) \\ \end{aligned} \right.$.

Theo đề bài ta có: $x_1.x_{2}^{2}-x_1( 5m+3x_2)=10 \, 115$ (3).

Từ $(1)$ suy ra $x_1=2-x_2$.

Thay vào $(2)$ và (3), ta có: $\left\{ \begin{aligned} & ( 2-x_2)x_2=-5m \\ & ( 2-x_2).x_{2}^{2}-( 2-x_2)( 5m+3x_2)=10 \, 115 \\ \end{aligned} \right.$

$\left\{ \begin{aligned} & 5m=x_{2}^{2}-2x_2\\ & ( 2-x_2).x_{2}^{2}-( 2-x_2)( x_{2}^{2}-2x_2+3x_2)=10 \, 115 \\ \end{aligned} \right.$

$\left\{ \begin{aligned} & 5m=x_{2}^{2}-2x_2 \\ & ( 2-x_2 ).x_{2}^{2}-( 2-x_2)( x_{2}^{2}+x_2)=10 \, 115 \\ \end{aligned} \right.$

$\left\{ \begin{aligned} & 5m=x_{2}^{2}-2x_2 \\ & 2x_{2}^{2}-x_{2}^{3}-2x_{2}^{2}-2x_2+x_{2}^{3}+x_{2}^{2}=10 \, 115 \\ \end{aligned} \right.$

$\left\{ \begin{aligned} & 5m=x_{2}^{2}-2x_2\\ & x_{2}^{2}-2x_2=10 \, 115 \\ \end{aligned} \right.$.

$5m=10 \, 115$

$m=2 \, 023$ (thỏa mãn).

Vậy $m=2 \, 023$ là giá trị cần tìm.

Hướng dẫn giải:

a) Thay $x=2, \, y=1$ vào phương trình đường thẳng $(d)$ ta có:

$1=2m.2+3-2m$

$2m=-2$

$m=-1$

Vậy $m=-1$ thỏa mãn yêu cầu.

b) Ta có phương trình hoành độ giao điểm $(d)$ và $(P)$: $x^2=2mx+3-2m$

$x^2-2mx+2m-3=0$ (*)

Ta có: $\Delta'=m^2-2m+3=(m-1)^2+2>0$ (với mọi $m$)

Nên phương trình (*) luôn có hai nghiệm phân biệt thì $(d)$ luôn cắt $(P )$ tại hai điểm phân biệt $A, \, B$.

Gọi $x_1; \, x_2$ là hoành độ các điểm $A, \, B$

Suy ra $x_1; \, x_2$ là hai nghiệm phân biệt của phương trình (*)

Mà $x_1; \, x_2$ là độ dài hai cạnh của một hình chữ nhật nên (*) có hai nghiệm phân biệt dương khi

$\left\{ \begin{aligned} & x_1+x_2>0 \\ & x_1x_2>0 \\ \end{aligned} \right.$

$\left\{ \begin{aligned} & 2m>0 \\ & 2m-3>0 \\ \end{aligned} \right.$

$m>\dfrac{3}{2}$

Áp dụng hệ thức Viète ta có: $x_1+x_2=2m; \, x_1x_2=2m-3$.

Vì $x_1; \, x_2$ là độ dài hai cạnh của một hình chữ nhật có đường chéo bằng $\sqrt{14}$ nên áp dụng định lí Pythagore trong tam giác vuông ta có :

$x_{1}^{2}+x_{2}^{2}=14$

$(x_1+x_2)^2-2x_1x_2=14$

$4m^2-2( 2m-3 )=14$

$2m^2+2m-4=0$

$m=-1$ (ktm); $m=2$ (tm)

Vậy $m=2$ là giá trị cần tìm.

Hướng dẫn giải:

a)

Đường thẳng $(d):\,y=3mx+1-m^2$ đi qua điểm $A( 1;-9 )$ thì

$-9=3m.1+1-{{m}^{2}}$

${{m}^{2}}-3m-9-1=0$

${{m}^{2}}-3m-10=0$

Phương trình có $\Delta = (-3)^2+4.10=49>0$

Suy ra phương trình có hai nghiệm phân biệt: $m_1=\dfrac{3+\sqrt{49}}{2}=5$; $m_2=\dfrac{3-\sqrt{49}}{2}=-2$.

Vậy $m=-2$; $m=5$ là các giá trị thỏa mãn bài toán

b) Phương trình hoành độ giao điểm của hai đồ thị hàm số đã cho là:

$x^2=3mx+1-m^2$

$x^2-3mx+m^2-1=0$ (*)

Để $( d )$ cắt $( P)$ tại hai điểm phân biệt của hoành độ $x_1;\,x_2$ thì phương trình (*) có hai nghiệm phân biệt $x_1;\,x_2$

$\Delta >0$

$(3m)^2-4(m^2-1)>0$

$9m^2-4m^2+4>0$

$5m^2+4>0$ với mọi $m$

Với mọi giá trị của $m$ thì $(d)$ luôn cắt $(P)$ tại hai điểm phân biệt của hoành độ $x_1;\,x_2$

Áp dụng hệ thức Viète với phương trình (*) ta có: $\left\{ \begin{aligned} & x_1+x_2=3m \\ &x_1x_2=m^2-1 \end{aligned} \right.$

Theo đề bài ra ta có:

$x_1+x_2=2x_1x_2$

$3m=2( m^2-1 )$

$2m^2-2-3m=0$

$2m^2-3m-2=0$

Phương trình có hai nghiệm phân biệt: $m_1=\dfrac{3+\sqrt{25}}{2.2}=2; \, m_2=\dfrac{3-\sqrt{25}}{2.2}=-\dfrac12$.

Vậy $m=-\dfrac12$; $m=2$ để thỏa mãn yêu cầu bài toán.

Hướng dẫn giải:

Phương trình hoành độ giao điểm của $(P)$ và $(d)$ là:

$x^2=( 2m+1 )x-2m$

$x^2-( 2m+1 )x+2m=0$

Ta có: $\Delta =\left[ -(2m+1)^2-4.2m \right] = 4m^2-4m+1 = ( 2m-1)^2$

Phương trình có hai nghiệm phân biệt khi $\Delta >0$

$2m-1\ne 0$

$m\ne \dfrac{1}{2}$

Theo hệ thức Viète ta có: $\left\{ \begin{aligned} & {{x}_{1}}+{{x}_{2}}=2m+1 \\ & {{x}_{1}}.{{x}_{2}}=2m \\ \end{aligned} \right.$

Khi đó: ${{y}_{1}}+{{y}_{2}}-{{x}_{1}}{{x}_{2}}=1$

$x_{1}^{2}+x_{2}^{2}-{{x}_{1}}{{x}_{2}}=1$

${{\left( {{x}_{1}}+{{x}_{2}} \right)}^{2}}-3{{x}_{1}}{{x}_{2}}=1$

${{\left( 2m+1 \right)}^{2}}-3.2m-1=0$

$4{{m}^{2}}+4m+1-6m-1=0$

$4{{m}^{2}}-2m=0$

$2m\left( 2m-1 \right)=0$

$2m=0$ hoặc $2m-1=0$

$m=0$ (thỏa điều kiện) hoặc $m=\dfrac{1}{2}$ (không thỏa điều kiện).

Vậy với $m=0$ thì $\left( P \right)$ cắt $\left( d \right)$ tại hai điểm phân biệt thỏa điều kiện đã cho.

Hướng dẫn giải:

Phương trình hoành độ giao điểm của $(P)$ và $(d)$ là:

$x^2-2(m-1)x+m-3=0$ (*)

Vì $x_1; \, x_2$ là hoành độ giao điểm của $(P)$ và $(d)$ nên $x_1; \, x_2$ là nghiệm của phương trình (*).

Do đó $\Delta '= (m-1)^2-(m-3) \ge 0$

$\Big( m-\dfrac{3}{2} \Big)^2+\dfrac{7}{4} \ge 0$ (luôn đúng)

Theo hệ thức Viète ta có: ${{x}_{1}}+{{x}_{2}}=2(m-1); \, {{x}_{1}}{{x}_{2}}=m-3$.

Khi đó: $M=x_{1}^{2}+x_{2}^{2}=( {{x}_{1}}+{{x}_{2}} )^2-2{{x}_{1}}{{x}_{2}}=4{{(m-1)}^{2}}-2. (m-3)=\dfrac{1}{4}{{(4m-5)}^{2}}+\dfrac{15}{4}\ge \dfrac{15}{4}$

Dấu "=" xảy ra khi và chỉ khi $m=\dfrac{5}{4}$

Vậy giá trị nhỏ nhất của biểu thức $M$ là $\dfrac{15}{4}$ khi $m=\dfrac{5}{4}$.