Bài học cùng chủ đề
- Tỉ số lượng giác của góc nhọn
- Khái niệm tỉ số lượng giác của một góc nhọn
- Tỉ số lượng giác của một góc nhọn đặc biệt
- Tỉ số lượng giác của hai góc phụ nhau
- Tỉ số lượng giác của góc nhọn
- Tỉ số lượng giác của các góc nhọn đặc biệt
- Tỉ số lượng giác của các góc phụ nhau
- Bài toán thực tế ứng dụng tỉ số lượng giác của góc nhọn
- Phiếu bài tập tuần 3. Tỉ số lượng giác của góc nhọn
Báo cáo học liệu
Mua học liệu
Mua học liệu:
-
Số dư ví của bạn: 0 coin - 0 Xu
-
Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu
Để nhận Coin\Xu, bạn có thể:

Tỉ số lượng giác của góc nhọn SVIP
1. Tỉ số lượng giác của một góc nhọn
a. Khái niệm
Cho góc nhọn α. Xét tam giác ABC vuông tại A có B =α.
⚡Tỉ số giữa cạnh đối và cạnh huyền được gọi là sin của góc α, kí hiệu sinα.
sinα = cạnh đối : cạnh huyền
⚡Tỉ số giữa cạnh kề và cạnh huyền được gọi là côsin của góc α, kí hiệu cosα.
cos α = cạnh kề : cạnh huyền
⚡Tỉ số giữa cạnh đối và cạnh kề được gọi là tang của góc α, kí hiệu tanα.
tanα = cạnh đối : cạnh kề
⚡Tỉ số giữa cạnh kề và cạnh đối được gọi là côtang của góc α, kí hiệu cotα.
cotα = cạnh kề : cạnh đối
Ví dụ 1. Tính các tỉ số lượng giác của góc B trong tam giác ABC.
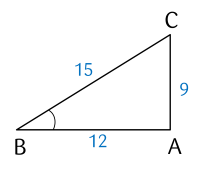
Lời giải
Xét tam giác ABC có A=90∘ và B là góc nhọn.
sinB=BCAC=159=0,6;
cos B=BCAB=1512=0,8;
tanB=ABAC=129=0,75;
cotB=ACAB=34.
b. Lưu ý
+ Khi không sợ nhầm lẫn, ta có thể viết sinB, cosB, tanB, cotB lần lượt thay cho các kí hiệu sinB, cosB, tanB, cotB.
+ Các tỉ số lượng giác của góc nhọn a luôn dương, sina<1; cosa<1 và cota=tana1.
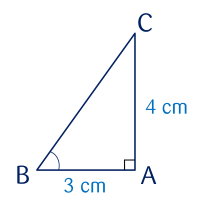
Cho tam giác ABC vuông tại A, có AB=3 cm, AC=4 cm. Tính các tỉ số lượng giác sinB, cosB, tanB.
Lời giải
Xét tam giác ABC vuông tại A, góc B nhọn.
Theo định lí Pythagore ta có: BC2=AC2+AB2=42+32=25 nên BC= cm.
Theo định nghĩa, ta có:
sinB= = ;
cosB= = ;
tanB= = .
(Kéo thả hoặc click vào để điền)
c) Tỉ số lượng giác của góc nhọn đặc biệt
| α | sinα | cosα | tanα | cotα |
| 30∘ | 21 | 23 | 33 | 3 |
| 45∘ | 22 | 22 | 1 | 1 |
| 60∘ | 23 | 21 | 3 | 33 |
Ví dụ 2. Tính giá trị của biểu thức P=tan45∘sin30∘.cos60∘.
Lời giải
P=tan45∘sin30∘.cos60∘=121.21=41.
Giá trị của sin30∘−cos60∘ bằng
2. Tỉ số lượng giác của hai góc phụ nhau
Định lí
Nếu hai góc phụ nhau thì sin góc này bằng côsin góc kia, tang góc này bằng côtang góc kia.
Với 0∘ <a<90∘ ta có:
⚡sin(90∘ − a)=cosa; ⚡cos(90∘ − a)=sina;
⚡tan(90∘ − a)=cota; ⚡cot(90∘ − a)=tana;
Ví dụ 3. Viết các tỉ số lượng giác sau thành tỉ số lượng giác của góc nhỏ hơn 45∘.
a) sin60∘;
b) cot82∘.
Lời giải
a) sin60∘=cos30∘;
b) cot82∘=tan8∘.
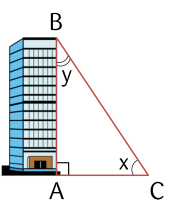
Tia nắng chiếu qua điểm B của nóc tòa nhà tạo với mặt đất một góc x và tạo với cạnh AB của tòa nhà một góc y. Cho biết cosx≈0,78 và cotx≈1,25. Tính siny+tany (làm tròn kết quả tới hàng phần trăm).
Trả lời:
Bạn có thể đăng câu hỏi về bài học này ở đây
