Biểu thức đại số biểu thị nửa tổng bình phương của \(a\) và \(b\) là:

\(\frac{1}{2} \left(\right. a^{2} + b^{2} \left.\right)\)

Trong đó, \(a^{2}\) là bình phương của \(a\), và \(b^{2}\) là bình phương của \(b\).

Bài 4:

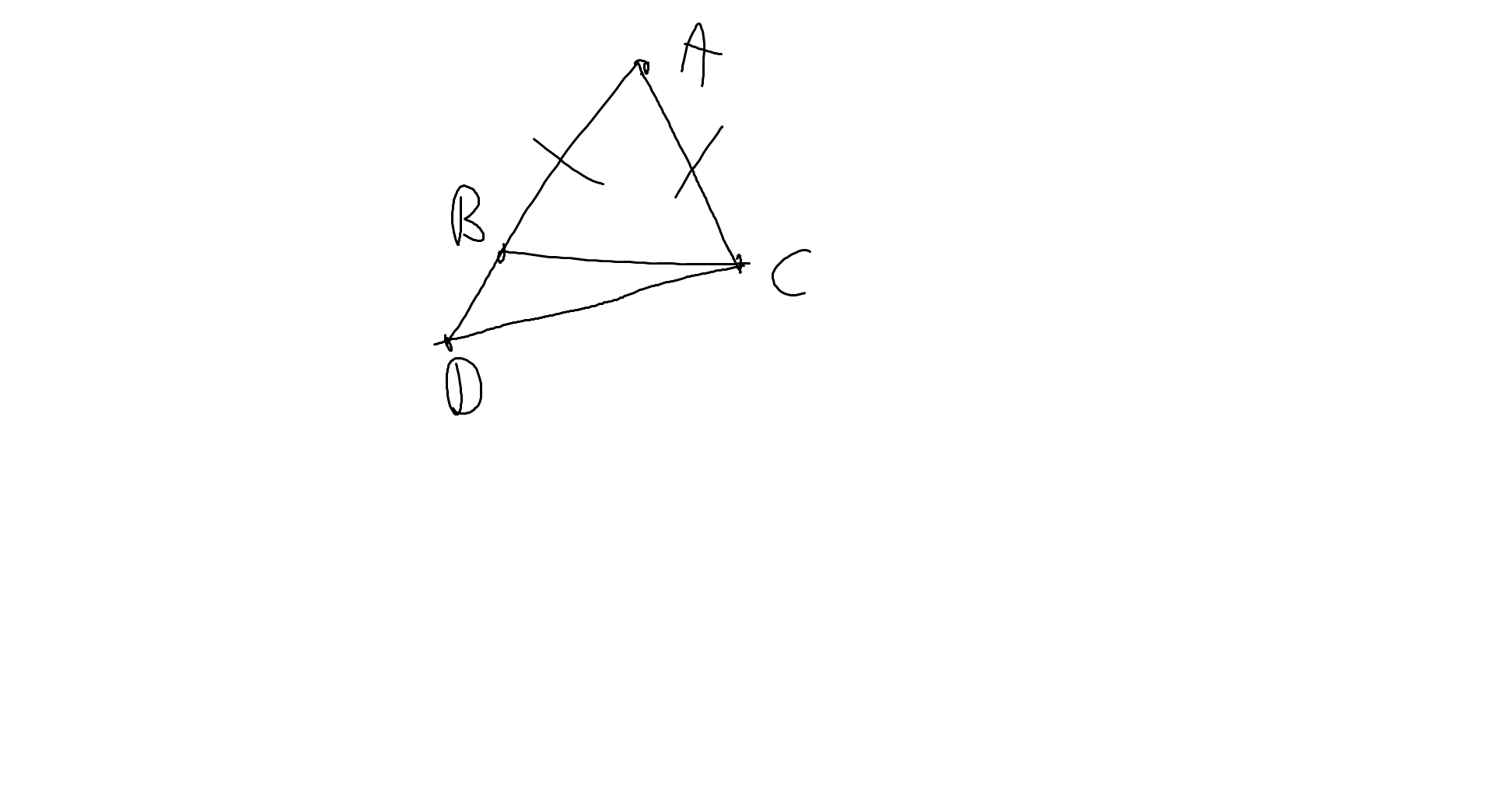
Xét ΔABC có \(\widehat{CBD}\) là góc ngoài tại đỉnh B

nên \(\widehat{CBD}=\widehat{BCA}+\widehat{BAC}\)

=>\(\widehat{CBD}>\widehat{ACB}\)

mà \(\widehat{ACB}=\widehat{ABC}\)(ΔABC cân tại A)

nên \(\widehat{CBD}>\widehat{CBA}\)

mà \(\widehat{CBD}+\widehat{CBA}=180^0\)

nên \(\widehat{CBD}>\dfrac{180^0}{2}=90^0\)

Xét ΔCBD có \(\widehat{CBD}>90^0\)

nên CD là cạnh lớn nhất trong ΔCBD

=>CD>CB

x là số tự nhiên à bạn

To solve the equation ∣x−10∣10+∣x−11∣11=1|x − 10|^{10} + |x - 11|^{11} = 1, we can start by examining the properties of the absolute value function and the exponents.

1. Case 1: x=10x = 10
2. • Substituting x=10x = 10, we have:

This satisfies the equation, so x=10x = 10 is a solution.

1. Case 2: x=11x = 11
2. • Substituting x=11x = 11, we have:

This satisfies the equation, so x=11x = 11 is another solution.

For any other value of xx between 10 and 11, the term ∣x−10∣10|x - 10|^{10} and ∣x−11∣11|x - 11|^{11} will not sum to 1 because both terms will be positive and greater than zero, making the sum greater than 1. Outside the range of 10 to 11, one of the terms will be raised to a very high power, making the sum exceed 1.

Therefore, the solutions to the equation ∣x−10∣10+∣x−11∣11=1|x - 10|^{10} + |x - 11|^{11} = 1 are:

\

3\(^{x+2}\) + 3\(^{x}\) - 23 = 949 - 2 x 3\(^{x}\)

3\(^2.\)3\(^{x}\) + 3\(^{x}\) + 2.3\(^{x}\) = 949 + 23

3\(^{x}\).(9 + 1 + 2) = 97

3\(^{x}\).(10 +2) = 97

3\(^{x}\).12 = 97

3\(^{x}\) = 97 : 12

3\(^{x}\) = 81

3\(^{x}\) = 3\(^4\)

\(x=4\)

Vậy \(x=4\)

cho mình hỏi tại sao dòng thứ 2 là 949 + 23 mà sang dòng thứ 3 là 97 vậy ạ , phải là 972 chứ @Nguyễn Thị Thương Hoài

Đây là toán nâng cao chuyên đề toán tỉ lệ thức, cấu trúc thi chuyên, thi học sinh giỏi các cấp. Hôm nay, Olm sẽ hướng dẫn các em giải chi tiết dạng này như sau:

Giải:

Gọi số máy cày đội một, đội hai, đội ba lần lượt là:

\(x;y;z\) (máy cày); \(x;y;z\in N\)*

Vì năng xuất của các máy và diện tích cánh đồng là như nhau nên ta có:

3\(x=5y=6z\)

5y = 6z ⇒ \(\frac{y}{6}=\frac{z}{5}\) = 1

Áp dụng tính chất dãy tỉ số bằng nhau ta có:

\(\frac{y}{6}=\frac{z}{5}=\frac{y-z}{6-5}=\) 1

y = 1.6 = 6 (máy cày)

z = 1.5 = 5 (máy cày)

3\(x\) = 5y = 5.6 = 30

\(3x=30\)

\(x=30:3\)

\(x=10\) (máy)

Vậy đội một, đội hai, đội ba lần lượt có số máy cày là: 10; 6; 5

Gọi \(x\) (máy), \(y\) (máy); \(z\) (máy) lần lượt là số máy cày của đội thứ nhất, đội thứ hai và đội thứ ba \(\left(x,y,z\in Z^+\right)\)

Do các máy cày có cùng năng suất và cày ba cánh đồng có cùng diện tích nên số máy cày và thời gian hoàn thành công việc là hai đại lượng tỉ lệ nghịch

\(\Rightarrow3x=5y=6z\)

\(\Rightarrow\dfrac{3x}{30}=\dfrac{5y}{30}=\dfrac{6z}{30}\)

\(\Rightarrow\dfrac{x}{10}=\dfrac{y}{6}=\dfrac{z}{5}\)

Do số máy cày của đội thứ hai nhiều hơn đội thứ ba 1 máy nên: \(y-z=1\)

Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:

\(\dfrac{x}{10}=\dfrac{y}{6}=\dfrac{z}{5}=\dfrac{y-z}{6-5}=\dfrac{1}{1}=1\)

\(\dfrac{x}{10}=1\Rightarrow x=10\) (nhận)

Vậy đội thứ nhất có 10 máy cày

\(B=\left(\dfrac{1}{2^2}-1\right)\left(\dfrac{1}{3^2}-1\right)\cdot...\cdot\left(\dfrac{1}{2025^2}-1\right)\)

\(=\left(\dfrac{1}{2}-1\right)\left(\dfrac{1}{3}-1\right)\cdot...\cdot\left(\dfrac{1}{2025}-1\right)\left(\dfrac{1}{2}+1\right)\left(\dfrac{1}{3}+1\right)\cdot...\cdot\left(\dfrac{1}{2025}+1\right)\)

\(=-\dfrac{1}{2}\cdot-\dfrac{2}{3}\cdot...\cdot\dfrac{-2024}{2025}\cdot\dfrac{3}{2}\cdot\dfrac{4}{3}\cdot...\cdot\dfrac{2026}{2025}\)

\(=\dfrac{1}{2025}\cdot\dfrac{2026}{2}=\dfrac{1013}{2025}\)

=-\(\left(\frac12\cdot\frac32\right)\cdot\left(\frac23\cdot\frac43\right)\ldots\left(\frac{2024}{2025}\cdot\frac{2026}{2025}\right)\)

=-\(\left(\frac{1}{2025}\cdot\frac{2026}{2}\right)\)

=-\(\frac{1013}{2025}\)

\(\frac{a}{3}\) = \(\frac{b}{4}\)

Áp dụng tính chất dãy tỉ số bằng nhau ta có:

\(\frac{a}{3}\) = \(\frac{b}{4}\) = \(\frac{a+b}{3+4}\) = \(\frac{21}{7}\) = 3

a = 3.3 = 9

b = 3.4 = 12

Vậy (a; b) = (9; 12)

A B C M K Q F E

Xét tam giác ABE và tam giác MBE

có BA=BM(GT)

BE chung 

AE=EM (GT)

suy ra tam giác ABE = tam giác MBE (c.c.c)

suy ra góc BEA=góc BEM , góc BAE=góc BME  (1)

Mà góc BEA + góc BEM=180độ

suy ra góc BEA =góc BEM=90độ

Xét tam giác EAK và tam giác EMK

có AE=EM (GT)

góc KEA=góc KEM = 90 độ

cạnh EK chung

suy ra tam giác EAK = tam giác EMK (cg.c)

suy ra góc KME=góc KAE (2) 

Từ (1) và (2) suy ra góc KME +góc EMB=góc KAE+ góc EAB

suy ra góc KMB=góc KAB = 90 độ 

suy ra KM vuông góc với BC

c) sai đề nhé

sao lại sai 

vì AB//HD nên ∠BAH=∠AHM (so le trong)và ∠BAH=∠CDM(đồng vị)
vì M là trung điểm HD nên HM=DM
xét △AHM và △CDM có
HM=DM
∠AHM=∠CDM(=∠BAH)
∠AMH=∠CMD(đối đỉnh)
Do đó △AHM=△CDM(gcg)
suy ra AM=CM hay M là trung điểm AC