\(\dfrac{1}{3}:\left|x-1\right|-0,25=\dfrac{5}{12}\\ \dfrac{1}{3\cdot\left|x-1\right|}-\dfrac{1}{4}=\dfrac{5}{12}\\ \dfrac{1}{3\cdot\left|x-1\right|}=\dfrac{2}{3}= >3\cdot\left|x-1\right|=\dfrac{3}{2}\\ =>\left|x-1\right|=\dfrac{1}{2}\\ =>\left[{}\begin{matrix}x-1=\dfrac{1}{2}=>x=\dfrac{3}{2}\\x-1=-\dfrac{1}{2}=>x=\dfrac{1}{2}\end{matrix}\right.\)

vậy x có 2 giá trị là x = 3/2 và x = 1/2

\(\frac13:\) |\(x\) - 1| - 0,25 = \(\frac{5}{12}\)

\(\frac13:\left|x-1\right|\) = \(\frac{5}{12}\) + 0,25

\(\frac13:\left|x-1\right|=\frac{5}{12}\) + \(\frac14\)

\(\frac13:\left|x-1\right|\) = \(\frac{5}{12}+\frac{3}{12}\)

\(\frac13:\left|x-1\right|=\frac23\)

|\(x-1\)| = \(\frac13:\frac23\)

|\(x-1\)| = \(\frac12\)

\(\left[\begin{array}{l}x-1=-\frac12\\ x-1=\frac12\end{array}\right.\)

\(\left[\begin{array}{l}x=-\frac12+1\\ x=\frac12+1\end{array}\right.\)

\(\left[\begin{array}{l}x=\frac12\\ x=\frac32\end{array}\right.\)

Vậy \(x\in\left\lbrace\frac12;\frac32\right\rbrace\)

Gọi số sản phẩm của hai công nhân làm được lần lượt là: \(x;y\) ( sản phẩm; \(x,y\) \(\in N\)*)
Ta có: \(\dfrac{x}{y}=0,95\)
\(\Rightarrow\dfrac{x}{y}=\dfrac{19}{20}\)
\(\Rightarrow\dfrac{x}{19}=\dfrac{y}{20}\) và \(y-x=10\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\dfrac{x}{19}=\dfrac{y}{20}=\dfrac{y-x}{20-19}=\dfrac{10}{1}=10\)
Do đó:
\(\dfrac{x}{19}=10\) nên \(x=10.19=190\)
\(\dfrac{y}{20}=10\) nên \(y=10.20=200\)
Vậy số sản phẩm của hai công nhân làm được lần lượt là: \(190\) sản phẩm; \(200\) sản phẩm.

a: \(A\left(x\right)=x^3+3x^2-5x-2x^2+5x^3+x^4-2x+1\)

\(=x^4+\left(x^3+5x^3\right)+\left(3x^2-2x^2\right)+\left(-5x-2x\right)+1\)

\(=x^4+6x^3+x^2-7x+1\)

Bậc là 4

Hệ số cao nhất là 1

Hệ số tự do là 1

b: \(B\left(x\right)=-x^6+2x^3+6-2x^4+x^6-x-5+2x^4+x^3\)

\(=\left(-x^6+x^6\right)+\left(-2x^4+2x^4\right)+\left(2x^3+x^3\right)+\left(-x\right)+\left(6-5\right)\)

\(=3x^3-x+1\)

Bậc là 3

Hệ số cao nhất là 3

Hệ số tự do là 1

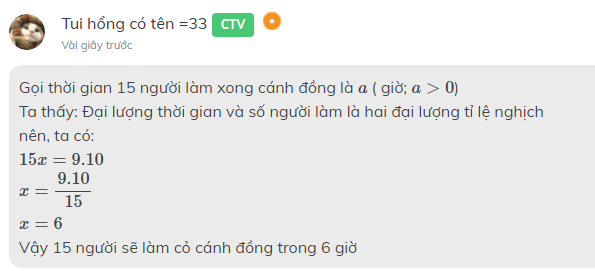
Gọi thời gian 15 người làm xong cánh đồng là \(a\) ( giờ; \(a>0\))
Ta thấy: Đại lượng thời gian và số người làm là hai đại lượng tỉ lệ nghịch
nên, ta có:
\(15x=9.10\)
\(x=\dfrac{9.10}{15}\)
\(x=6\)
Vậy 15 người sẽ làm cỏ cánh đồng trong 6 giờ 

\(\left(\dfrac{-5}{8}+\dfrac{6}{17}\right).\dfrac{3}{2}+\left(\dfrac{-3}{8}+\dfrac{11}{17}\right).\dfrac{3}{2}\)
\(=\left(\dfrac{-5}{8}+\dfrac{6}{17}+\dfrac{-3}{8}+\dfrac{11}{17}\right).\dfrac{3}{2}\)
\(=\left[\left(\dfrac{-5}{8}-\dfrac{3}{8}\right)+\left(\dfrac{6}{17}+\dfrac{11}{17}\right)\right].\dfrac{3}{2}\)
\(=\left[\dfrac{-8}{8}+\dfrac{17}{17}\right].\dfrac{3}{2}\)
\(=\left[-1+1\right].\dfrac{3}{2}\)
\(=0.\dfrac{3}{2}=0\)

Gọi số tờ tiền Hoa, Mai, Minh được thưởng lần lượt là a(tờ),b(tờ),c(tờ)

(Điều kiện: \(a,b,c\in Z^+\))

Số tiền thưởng ba bạn nhận được là như nhau nên ta có:

2a=5b=10c

=>\(\dfrac{2a}{10}=\dfrac{5b}{10}=\dfrac{10c}{10}\)

=>\(\dfrac{a}{5}=\dfrac{b}{2}=\dfrac{c}{1}\)

Tổng số tờ tiền ba bạn được nhận là 56 tờ nên a+b+c=56

Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

\(\dfrac{a}{5}=\dfrac{b}{2}=\dfrac{c}{1}=\dfrac{a+b+c}{5+2+1}=\dfrac{56}{8}=7\)

=>\(\left\{{}\begin{matrix}a=7\cdot5=35\\b=7\cdot2=14\\c=7\cdot1=7\end{matrix}\right.\left(nhận\right)\)

Vậy: số tờ tiền Hoa, Mai, Minh được thưởng lần lượt là 35(tờ),14(tờ),7(tờ)

a: Xét ΔOAC vuông tại A và ΔOBE vuông tại B có

OA=OB

\(\widehat{AOC}=\widehat{BOE}\)(hai góc đối đỉnh)

Do đó: ΔOAC=ΔOBE

=>OC=OE và AC=BE

Xét ΔDOC vuông tại O và ΔDOE vuông tại O có

DO chung

OC=OE

Do đó: ΔDOC=ΔDOE

=>DC=DE

=>DC=DB+BE=DB+AC

b: Ta có: CH//AB

AB\(\perp\)BD

Do đó: CH\(\perp\)BD

Xét ΔCEH có

HO,ED là các đường cao

HO cắt ED tại D

Do đó: D là trực tâm của ΔCEH

=>CD\(\perp\)HE