một con lắc lò xo dao động điều hòa thực hiện được 100 dao động hết thời gian 31,4 giây chọn gốc thời gian tại t = 0 khi vật đi qua vị trí x = 2 đang chuyển động ra xa vị trí cân bằng với vận tốc 40 căn 3 tìm x,v,a tại thời điểm t=pi/10
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

d) \(A=3cm\); \(\omega=4\pi\left(rad/s\right)\); \(\varphi_0=\dfrac{\pi}{5}\left(rad\right)\)
Khi đó \(T=\dfrac{2\pi}{\omega}=0,5\left(s\right)\)
Cho \(x=1,5cm\Leftrightarrow\varphi=\pm\dfrac{\pi}{3}\left(rad\right)\)
Thời gian vật đi qua vị trí \(x=1,5cm\) lần thứ ba là:
\(T+t_d=0,5+\dfrac{\Delta\varphi_d}{2\pi}.T\)
\(=0,5+\dfrac{\dfrac{\pi}{3}-\dfrac{\pi}{5}}{2\pi}.0,5\)
\(=\dfrac{8}{15}\left(s\right)\)
e) Thời gian cần tìm là:
\(t_e+19T=\dfrac{\Delta\varphi_e}{2\pi}.T+19.0,5\)
\(=\dfrac{\dfrac{4\pi}{3}}{2\pi}.0,5+9.5=\dfrac{59}{6}\left(s\right)\)

Đối với dao động cơ điều hòa của một chất điểm thì khi chất điểm đi đến vị trí biên nó có tốc độ bằng không và gia tốc cực đại.

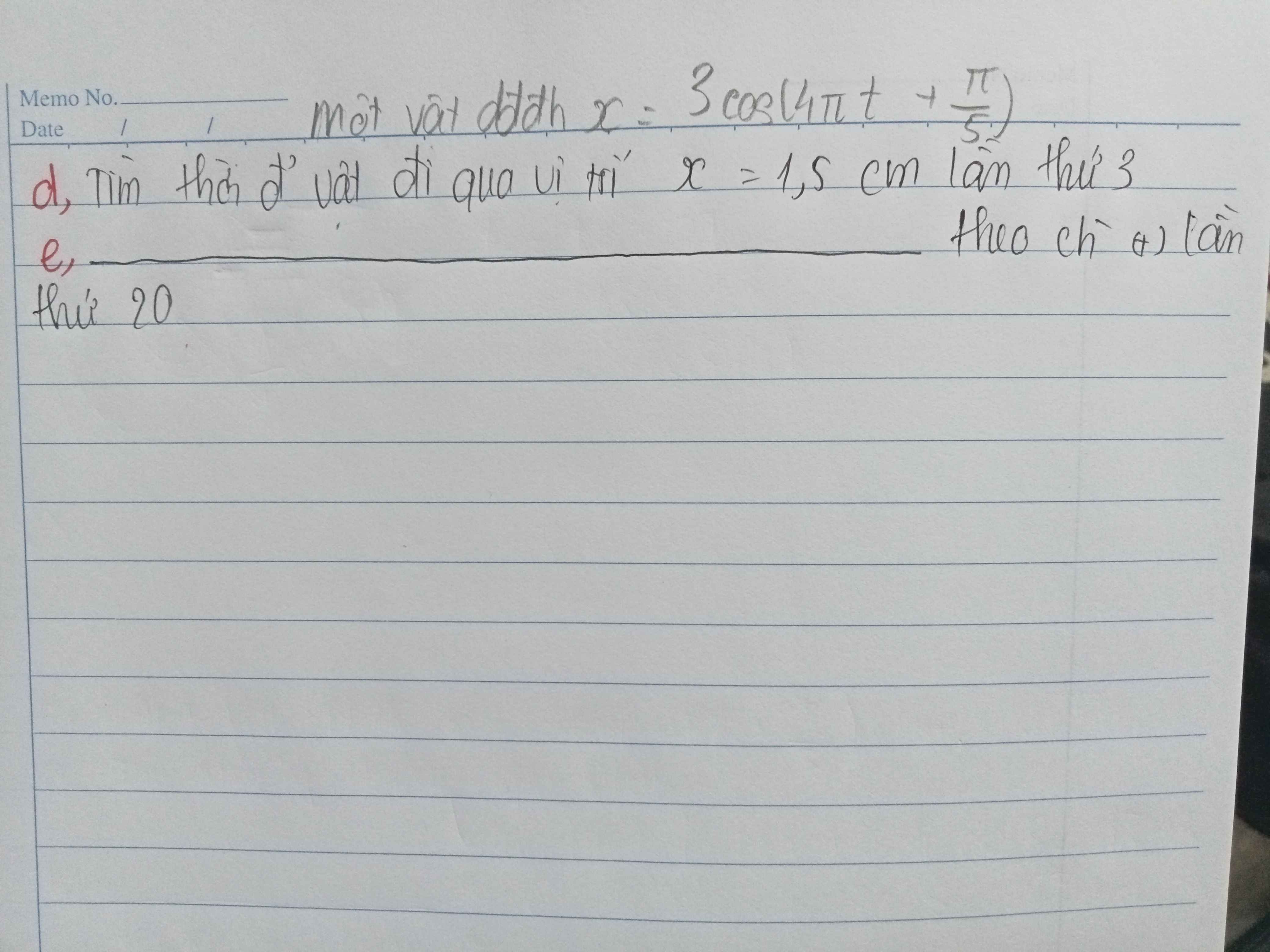

`T=pi/10(s)=> \omega =20 (rad//s)`
`@A=\sqrt{2^2 +[(40\sqrt{3})^2]/[20^2]}=4(cm)`
Vì tại thời điểm `t=\pi/10` trùng với thời điểm `t=0`
`=>{(x=2(cm)),(v=40\sqrt{3}(cm//s)),(a=-\omega ^2 .x=-800(cm//s^2)):}`