Căn bậc hai số học của $9$ là

Chọn câu sai. Cho hình trụ có bán kính đáy là $R$ và chiều cao $h$. Khi đó

Phương trình nào dưới đây là phương trình bậc hai một ẩn?

Trong các bất phương trình sau, bất phương trình bậc nhất một ẩn là

Cho tam giác $ABC$ vuông tại $A$; đường cao $AH$. Biết $AB = 6$; $AH = 4,8$ thì giá trị của $\sin B$ là

Kí hiệu X là kết quả đồng xu được mặt xanh, Đ là kết quả đồng xu được mặt đỏ. Không gian mẫu của phép thử gieo $2$ lần một đồng xu có $1$ mặt xanh và $1$ mặt đỏ là

Bạn An phỏng vấn một số bạn học sinh cùng trường về loại nước uống yêu thích nhất. Kết quả được cho ở bảng sau:

Tần số tương đối biểu diễn mẫu số liệu điều tra về trà sữa là

Hệ phương trình nào dưới đây là hệ hai phương trình bậc nhất hai ẩn?

Rút gọn biểu thức: $\Big( \dfrac{a\sqrt{a}}{\sqrt{a}-1}+\dfrac{1}{1-\sqrt{a}} \Big).\dfrac{\sqrt{a}-1}{a\sqrt{a}+a-\sqrt{a}}$ (với $a>0$, $a\ne 1$)

Cho $a \lt b$. Chứng minh rằng $- 2a - 5 > - 2b - 5$.

Cho phương trình $x^2 - x - 10 = 0$. Chứng tỏ phương trình có hai nghiệm phân biệt $x_1$, $x_2$. Không giải phương trình, tính $x_1^3+x_2^{3}$.

Giải hệ phương trình sau: $\left\{ \begin{aligned} & x+2y=1 \\ & x-y=-2 \end{aligned} \right.$.

Cô giáo muốn chọn $2$ trong số $4$ bạn: Xuân, Hạ, Thu, Đông vào đội sao đỏ của trường. Tính xác suất của biến cố “có bạn Hạ trong đội sao đỏ".

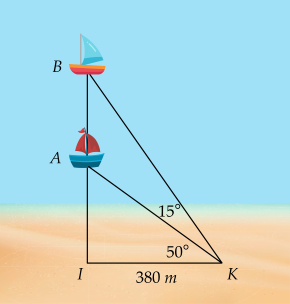
Hai chiếc thuyền $A$ và $B$ ở vị trí được minh họa như hình dưới dây. Tính khoảng cách giữa chúng. (kết quả làm tròn đến hàng đơn bị của mét)

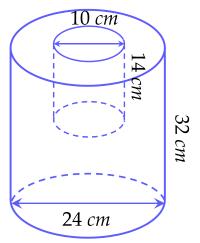
Một hình trụ có đường kính đáy $24$ cm và chiều cao $32$ cm, người ta khoét bỏ một hình trụ có đường kính đáy $10$ cm và chiều cao $14$ cm. (hình vẽ). Người ta sơn toàn bộ các mặt của phần còn lại của hình trụ. Tính diện tích được phủ sơn (kết quả làm tròn đến hàng đơn vị)

Cho đường tròn tâm $O$ đường kính $BC$, trên tia đối của tia $BC$ lấy điểm $A$. Từ $A$ kẻ tiếp tuyến $AM$ đến đường tròn $(O)$ ($M$ là tiếp điểm). Trên cung nhỏ $MC$ lấy điểm $E$ bất kỳ, đường thẳng $AE$ cắt đường tròn $(O)$ tại điểm thứ hai là $F \,(F$ không trùng $E$). Gọi $I$ là chân đường vuông góc kẻ từ điểm $O$ đến $EF$.

a) Chứng minh tứ giác $AMIO$ nội tiếp được trong một đường tròn.

b) Gọi $H$ là hình chiếu vuông góc của $M$ lên đường thẳng $BC$. Chứng minh: $\widehat{OFH}=\widehat{OAF}$.

c) Gọi $G$ là trọng tâm của $\Delta OFE$. Chứng minh rằng khi điểm $E$ thay đổi trên cung nhỏ $MC$ thì điểm $G$ luôn thuộc một đường tròn cố định.

Một công ty tư nhân tại Thành phố A dự định thuê một số xe lớn cùng loại để chở vừa hết $210$ người đi du lịch Thành phố B. Nhưng thực tế, công ty lại thuê toàn bộ xe nhỏ hơn cùng loại. Biết rằng số xe nhỏ phải thuê nhiều hơn số xe lớn là $2$ chiếc thì mới chở vừa hết số người trên và mỗi xe nhỏ chở ít hơn mỗi xe lớn là $12$ người. Tính số xe nhỏ đã thuê.