$\sqrt{(\sqrt{3}-2)^2}$ bằng

Nếu $2a - 3 > 2b - 3$ thì

Lớp 9A có $40$ học sinh, trong đó có $6$ học sinh cận thi. Gặp ngẫu nhiên một học sinh của lớp, xác suất thực nghiệm của biến cố “Học sinh đó không bị cận thị” là

Phương trình bậc hai $x^2 -2x +m =0$ có hai nghiệm phân biệt nếu

Hệ phương trình $\left\{ \begin{aligned} & mx-4y=6 \\ & x-my=3 \end{aligned} \right.$ (với $m$ là tham số) có vô số nghiệm khi

Cho tam giác $\Delta ABC$ vuông tại $A$, khi đó giá trị lượng giác $\tan \widehat{ABC}$ bằng

Quả bóng rổ sử dụng trong thi đấu có dạng hình cầu với đường kính bằng $24$ cm. Thể tích của quá bóng là

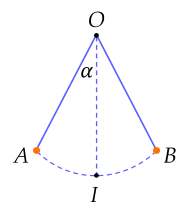
Một con lắc di chuyển từ vị trí $A$ đến vị trí $B$. Biết rằng sợi dây $OA$ có độ dài bằng $l$ và tia $OA$ tạo với phương thẳng đứng góc $\alpha$, khi đó độ dài quãng đường $AB$ mà con lắc đó đã di chuyển là

Cho biểu thức $P=\dfrac{2\sqrt{x}+3}{\sqrt{x}+3}+\dfrac{3\sqrt{x}-2}{\sqrt{x}-1}-\dfrac{15\sqrt{x}-11}{x+2\sqrt{x}-3}$ (với $x\ge 0;x\ne 1$)

a) Rút gọn $P$

b) Tìm giá trị nhỏ nhất của $P$.

Giải phương trình $x^2+x-2=0$.

Giải hệ phương trình: $\left\{ \begin{aligned} & 3x+2y=4 \\ & x-y=3 \end{aligned} \right.$

Cho phương trình $x^2+mx+m-3=0$ với $m$ là tham số, chứng minh phương trình luôn có hai nghiệm phân biệt $x_1,x_2$ với mọi giá trị của $m$. Tìm $m$ để $x_1,\,x_2$ thỏa mãn $x_1^2-mx_2+x_1.x_2=2$.

Một chiếc cổng chào được thiết kế có hình dạng như đồ thị $(P)$ của hàm số $y = ax^2$ ($a$ là hằng số, $a \lt 0$) như hình vẽ. Biết $AB = 4$ m, chiều cao cánh cổng là $OC = 8$ (m).

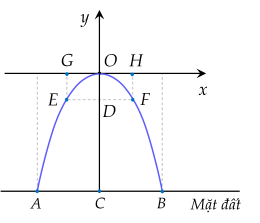
a) Xác định hằng số $a$.

b) Tại vị trí cách mặt đất một đoạn $CD = 6$ m, người ta đặt một thanh gỗ song song với mặt đất, hai đầu mút của thanh gỗ là hai điểm $E$, $F$ thuộc $(P)$. Tính chiều dài của thanh gỗ.

Tọa lạc ở làng Phú Gia, xã Cát Tường, huyện Phù Cát, tỉnh Bình Định, làng nón ngựa Phú Gia với hơn 300 năm tuổi nghề làm nón ngựa, một sản phẩm dẻo dai, bền bỉ hệt như những con người nơi đây. Nếu chiếc nón bài thơ xứ Huế nổi tiếng với những hoa văn long phượng được lồng ghép cùng những câu thơ, câu văn thơ mộng, mềm mại thì chiếc nón ngựa có nét mạnh mẽ của người con đất võ với những hình ảnh khảng khái, cứng cỏi “long, lân, quy, phượng”, “mai, lan, cúc, trúc” hay “lưỡng long tranh châu”,…Làm nón ngựa rất công phu phải trải qua 3 công đoạn. Đó là làm mê sườn, đan sườn mê và chằm nón. Mỗi công đoạn có một thôn, một xóm làm riêng theo hình thức chuyên môn hóa.

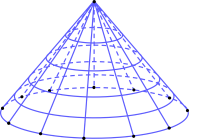
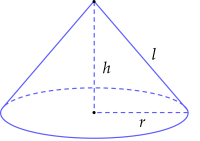
Khung của nón ngựa có dạng hình nón được làm bởi các thanh gỗ nối từ đỉnh tới đáy như các đường sinh (ℓ), nhiều vành nón được làm từ những thanh tre mảnh nhỏ, dẻo dai uốn thành những vòng tròn có đường kính to, nhỏ khác nhau, cái nhỏ nhất to bằng đồng xu.

+ Đường kính $(d = 2r)$ của chiếc nón ngựa khoảng $40$ (cm);

+ Chiều cao $(h)$ của chiếc nón ngựa khoảng $19$ (cm).

a) Tính độ dài của thanh tre uốn thành vòng tròn lớn nhất của vành chiếc nón ngựa (không kể phần chắp nối, tính gần đúng đến 2 chữ số thập phân).

b) Tính diện tích phần lá phủ xung quanh của chiếc nón ngựa (không kể phần chắp nối, tính gần đúng đến 2 chữ số thập phân).

Mẫu số liệu dưới đây ghi lại độ dài quãng đường di chuyển trong một tuần (đơn vị: kilômét) của $60$ chiếc ô tô:

Ghép các số liệu trên thành năm nhóm sau: $[100; 120)$, $[120; 140)$, $[140; 160)$, $[160; 180)$, $[180; 200)$.

a) Tìm tần số của mỗi nhóm đó. Lập bảng tần số ghép nhóm của mẫu số liệu ghép nhóm đó.

b) Tìm tần số tương đối của mỗi nhóm đó. Lập bảng tần số tương đối ghép nhóm của mẫu số liệu ghép nhóm đó.

Vẽ biểu đồ tần số tương đối ghép nhóm ở dạng biểu đồ cột và biểu đồ đoạn thẳng của mẫu số liệu ghép nhóm đó.

Một bác nông dân dự định đào một hồ cá hình chữ nhật. Nếu tăng chiều rộng lên $2$ m, giảm chiều dài đi $3$ m thì diện tích tăng thêm $4$ m². Nếu giảm chiều rộng đi $3$ m, tăng chiều dài thêm $2$ m thì diện tích hồ cá giảm đi $46$ m². Tính diện tích hồ cá mà bác dự định đào.

Cho $\Delta ABC$ nhọn nội tiếp đường tròn $(O;R)$. Vẽ đường cao $BI$, $CK$ của $\Delta ABC$ cắt nhau tại $H$.

a) Chứng minh bốn điểm $B$, $C$, $I$, $K$ cùng thuộc một đường tròn, xác định tâm $M$ của đường tròn đó.

b) Vẽ đường kính $AD$. Chứng minh ba điểm $H$, $M$, $D$ thẳng hàng.

c) Cho $\widehat{BAC}=60^\circ$. Chứng minh rằng $AH=R$.