Đề số 2 thi thử vào 10 năm 2025 (Cấu trúc 20% trắc nghiệm + 80% tự luận) SVIP

Điều kiện xác định của biểu thức $\dfrac{2\,025+x^2}{\sqrt{x-1}}$ là

Cho hàm số $y=-5x^2.$ Đồ thị hàm số đi qua điểm nào sau đây?

Biết $(x_0;y_0)$ là một nghiệm của hệ phương trình $\left\{ \begin{aligned} & x+y=5\\ & 2y-x=4 \end{aligned} \right.$. Khi đó biểu thức $S=3x_0-2y_0$ có giá trị bằng

Cho đường tròn $(O)$ bán kính $R=15$ cm và đường tròn $(O')$ bán kính $R=6$ cm. Biết độ dài đoạn nối tâm $OO'=9$ cm thì số điểm chung của hai đường tròn là

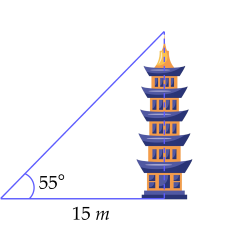
Một tòa tháp có bóng trên mặt đất dài $15$ m, biết rằng góc tạo bởi tia nắng mặt trời với mặt đất là $55^\circ$. Chiều cao của tòa tháp (làm tròn đến chữ số thập phân thứ hai) bằng

Một hình quạt tròn $OAB$ của đường tròn $(O,R)$ có diện tích $\dfrac{5\pi R^2}{24}$. Vậy sđ$\overset\frown{\,AB}$ bằng

Xếp $3$ quyển sách khác loại vào một kệ sách. Số cách xếp là

Nam có một hộp đồ chơi trong đó có $2$ bi đỏ, $3$ bi xanh, các viên bi cùng hình dạng và kích thước. Nam cho em trai lấy ngẫu nhiên $2$ viên bi từ hộp. Xác suất của biến cố "$2$ viên bi lấy ra khác màu" bằng

Rút gọn biểu thức $P=\dfrac{x+1}{2\sqrt{x}-2}-\dfrac{\sqrt{x}}{\sqrt{x}-1}$ với $x\ge 0,\,x\ne 1.$

Bạn Nam thống kê lại độ dài quãng đường (đơn vị: km) mình chạy bộ mỗi ngày trong tháng $11$ theo bảng tần số tương đối ghép nhóm sau:

a) Tìm nhóm có tần số tương đối ghép nhóm lớn nhất.

b) Vẽ biểu đồ hình quạt biểu diễn bảng tần số trên.

Trên mặt phẳng tọa độ $Oxy$, cho điểm $A(-4;\,32)$ thuộc đồ thị hàm số $y=(a-1)x^2.$

a) Tìm $a$.

b) Với $a$ vừa tìm được, tìm các điểm thuộc đồ thị hàm số có tung độ bằng $4$.

Cho phương trình $x^2-7x+12=0$ có hai nghiệm phân biệt $x_1;\,x_2$. Không giải phương trình, hãy tính giá trị của biểu thức $M=(1-2\,025x_1)x_1-x_2(2\,025x_2-x_1-1).$

Giải bài toán bằng cách lập phương trình hoặc hệ phương trình.

Sau thiệt hại nặng nề của cơn bão Yagi gây ra, một trường trung học cơ sở đã quyên góp tiền để mua $1\,500$ quyển vở gồm hai loại để chia thành các phần quà tặng cho các em học sinh làng Nủ, xã Bảo Khánh, huyện Bảo Yên, tỉnh Lào Cai. Giá bán của mỗi quyển vở loại thứ nhất và loại thứ hai lần lượt là $18\,000$ đồng và $20\,000$ đồng. Hỏi nhà trường đã mua bao nhiêu quyển vở mỗi loại? Biết rằng số tiền nhà trường đã dùng để mua $1\,500$ quyển vở đó là $29$ triệu đồng.

Một chiếc kem ốc quế có dạng hình nón với phần vỏ quế có đường kính đáy là $4,4$ cm và chiều cao vỏ quế là $12$ cm. (Lấy $\pi = 3,14$ và làm tròn kết quả đến hàng đơn vị).

a) Tính thể tích của chiếc kem ốc quế.

b) Người ta lấy phần kem từ một hộp hình trụ có chiều cao là $15$ cm, với diện tích đáy $100\pi$ cm² để cho vào vỏ ốc quế. Có thể lấy kem từ hộp làm được tối đa bao nhiêu chiếc kem ốc quế (coi phần vỏ kem có độ dầy không đáng kể)?

Cho đường tròn $(O;R)$, dây $AB$ khác đường kính. Kẻ $OH$ vuông góc với $AB$ tại $H$. Đường thẳng $OH$ cắt tiếp tuyến tại $A$ của đường tròn ở điểm $M$.

a) Chứng minh tứ giác $AMBO$ nội tiếp đường tròn.

b) Kẻ đường kính $AC$ của đường tròn $(O)$, tiếp tuyến tại $C$ của đường tròn $(O)$ cắt $MB$ ở $N$. Kẻ $BQ$ vuông góc với $AC$ tại $Q$. Chứng minh $\dfrac{QM}{QM+QN}=\dfrac{BM}{MN}$.