Phương trình $(x-2)(x-3)=0$ có nghiệm là

Nghiệm của bất phương trình $12-3x\le 0$ là

Điều kiện xác định của biểu thức $\sqrt{2x-4}$ là

Rút gọn biểu thức $C=\sqrt[3]{8a^3}-6a$ ta được kết quả là

Trong mặt phẳng tọa độ $Oxy$ cho parabol $(P): y=x^2$ và đường thẳng $(d): y=2x-m+3$. Giá trị $m$ để đường thẳng $(d)$ cắt $(P)$ tại $2$ điểm phân biệt là

Đồ thị hàm số $y=ax^2$ đi qua điểm $A(3;\,12)$. Khi đó $a$ bằng

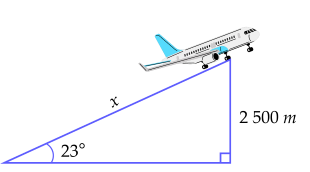
Một máy bay cất cánh theo phương hợp với mặt đất một góc $23^\circ.$ Hỏi muốn đạt độ cao $2\, 500$ m, máy bay phải bay một đoạn đường $x$ dài bao nhiêu mét? (làm tròn kết quả đến hàng đơn vị)

Thể tích $V$ của hình cầu có bán kính $R=3$ cm là

Lương của các công nhân một nhà máy được cho trong bảng sau:

Để vẽ biểu đồ tẩn số tương đối ghép nhóm dạng đoạn thẳng, ta dùng giá trị nào đại diện cho nhóm số liệu $[9;11)$?

Bạn Nam gieo một con xúc xắc $10$ lần liên tiếp thì thấy mặt $4$ chấm xuất hiện $3$ lần. Xác suất thực nghiệm xuất hiện mặt $4$ chấm là

Cho $\Delta ABC$ có $\widehat{BAC} = 45^\circ$ nội tiếp trong đường tròn tâm $O$ bán kính $2$ cm. Diện tích tam giác $OBC$ bằng

Rút gọn biểu thức: $B=\Big(\dfrac{1}{\sqrt{x}}+\dfrac{1}{3-\sqrt{x}} \Big):\dfrac{1}{3-\sqrt{x}}$ với $x>0,\,x\ne 9$.

Giải hệ phương trình sau: $\left\{ \begin{aligned}&2x-3y=7\\&x+5y=-3 \end{aligned} \right.$

Giải phương trình: $2x^2-3x-5=0$.

Cho phương trình $x^2-2(m-1)x+m^2=0$. Tìm $m$ để phương trình có hai nghiệm phân biệt $x_1;\,x_2$ thỏa mãn: $\dfrac{x_{1}^{2}}{x_2}+\dfrac{x_2^2}{x_1}=-5 (x_2+x_1)$

Cho $\Delta ABC$ có ba góc nhọn nội tiếp đường tròn $(O;\,R)$. Các đường cao $AD$, $BF$, $CE$ của $\Delta ABC$ cắt nhau tại $H$.

a) Chứng minh tứ giác $BEHD$ nội tiếp một đường tròn.

b) Kéo dài $AD$ cắt đường tròn $(O)$ tại điểm thứ hai $K$. Kéo dài $KE$ cắt đường tròn $(O )$ tại điểm thứ hai $I$. Gọi $N$ là giao điểm của $CI$ và $EF$. Chứng minh $CE^2=CN.CI$.

c) Kẻ $OM$ vuông góc với $BC$ tại $M$. Gọi $P$ là tâm đường tròn ngoại tiếp $\Delta AEF$. Chứng minh ba điểm $M$, $N$, $P$ thẳng hàng.

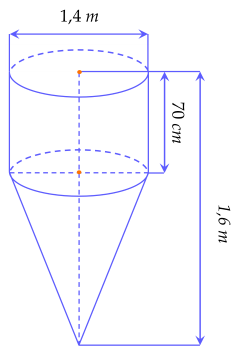
Một dụng cụ trộn bê tông gồm một phần có dạng hình trụ, phần còn lại có dạng hình nón. Các kích thước cho trên hình. Tính thể tích của dụng cụ này (độ chính xác $0,005$)

Cho $a$, $b$, $c$ thực dương thỏa mãn $abc=1$. Chứng minh rằng:

$\dfrac{1}{\sqrt{a^4-a^3+ab-2}}+\dfrac{1}{\sqrt{b^4-b^3+bc+2}}+\dfrac{1}{\sqrt{c^4+c^3+ac+2}}\le \sqrt{3}$