Phương trình $(2x+8)(x-3)=0$ có tập nghiệm là

Nghiệm của bất phương trình $\dfrac{5x+3}{4} \lt \dfrac{4x-5}{3}$ là

Điều kiện xác định của $\sqrt{2x-5}$ là

Giá trị của biểu thức $\dfrac{2-\sqrt{5}}{2+\sqrt{5}}$ là

Trong mặt phẳng tọa độ $Oxy$ cho đường thẳng $(d)$ có phương trình $y=(m^2-3)x+5$. Giá trị $m$ để $(d)$ song song với đường thẳng $(d'): y=x-m+3$ bằng

Trong mặt phẳng tọa độ $Oxy$ cho Parabol $(P):y=ax^2$. Điểm $A\left(1;2 \right)\in (P)$. Giá trị của $a$ là

Cho tam giác $ABC$ vuông cân tại $A$, khi đó giá trị lượng giác $\sin \widehat{ABC}$ là

Một bình đựng nước hình trụ có đường kính đáy là $8$ cm và chiều cao là $25$ cm. Thể tích của bình là bao nhiêu? (Lấy $\pi =3,14$)

Gieo một con xúc xắc đồng chất $100$ lần kết quả được ghi lại như sau:

Có bao nhiêu lần số chấm nhỏ hơn $4$ xuất hiện?

Xác suất thực nghiệm của sự kiện $A$ sau $n$ hoạt động vừa thực hiện là $\dfrac{n(A)}{n}$ thì $n(A)$ được gọi là

Giá trị của biểu thức $\dfrac{2-\sqrt{5}}{2+\sqrt{5}}$ là

Giá trị của $M=\sqrt{1,69.1,38-1,69.0,74}$ là

Cho $A=\Big( \dfrac{\sqrt{x}-1}{\sqrt{x}+1}-\dfrac{\sqrt{x}+1}{\sqrt{x}-1}-\dfrac{4x}{x-1} \Big) : \Big( 1-\dfrac{\sqrt{x}-4}{2\sqrt{x}-2} \Big)$ (với $x\ge 0,\,x\ne 1$).

a) Rút gọn biểu thức $A$.

b) Tìm các giá trị của $x$ để $A>-1$.

Giải hệ phương trình $\left\{ \begin{aligned} & 2x+3y=-1 \\ & 2x-y=-5 \end{aligned} \right.$

Giải phương trình $x^2-4x+3=0$.

Cho phương trình $x^2-(m+2)x-3=0 \,\, (1)$ ($m$ là tham số). Chứng minh phương trình luôn có hai nghiệm phân biệt $x_1,x_2$ với mọi giá trị của $m$. Tìm $m$ để $x_1,x_2$ thỏa mãn $\sqrt{\dfrac{x_{1}^{2}-mx_1+1}{x_{2}^{2}-mx_2+1}}=\dfrac{-x_1}{x_2}$.

Bác Dũng có một cái khóa số như hình bên. Bác Dũng chọn ngẫu nhiên một dãy gồm $4$ chữ số để đặt làm mã số mở khóa. Tính xác suất của các biến cố:

a) $A$: “$4$ chữ số được chọn giống nhau”;

b) $B$: “$4$ chữ số được chọn lập thành một số có $4$ chữ số”;

c) $C$: “$4$ chữ số được chọn có tổng bằng $35$”.

Nước giải khát thường được đựng trong lon nhôm và cỡ lon phổ biến trên thế giới thường chứa khoảng $335$ ml chất lỏng, được thiết kế hình trụ với chiều cao gần gấp đôi đường kính đáy (cao $12$ cm, đường kính đáy $6,5$ cm). Nhưng hiện nay các nhà sản xuất có xu hướng tạo ra những lon nhôm với kiểu dáng thon dài cao. Tuy chi phí sản xuất của những chiếc lon này tốn kém hơn, do nó có diện tích mặt ngoài lớn hơn, nhưng nó lại dễ đánh lừa thị giác và được người tiêu dùng ưa chuộng hơn.

a) Một lon nước ngọt cao $14$ cm, đường kính đáy là $6$ cm. Hỏi lon nước ngọt cao này có thể chứa được hết lượng nước ngọt của một lon có cỡ phổ biến không? Vì sao?

(kết quả làm tròn đến hàng đơn vị)

b) Biết chi phí sản xuất một lon tỉ lệ thuận với diện tích toàn phần của lon. Hỏi chi phí sản xuất lon nước ngọt cao ở câu a) tăng bao nhiêu phần trăm so với chi phí sản xuất lon có cỡ phổ biến?

(Biết $S_{tp}=2\pi rh+2\pi r^2$, kết quả làm tròn đến hàng phần mười)

Cho đường tròn $(O)$, bán kính $R\,(R>0)$ và dây cung $BC$ cố định. Một điểm $A$ chuyển động trên cung lớn $BC$ sao cho tam giác $ABC$ có ba góc nhọn. Kẻ các đường cao $AD$, $BE$ của tam giác $ABC$ cắt nhau tại $H$ và $BE$ cắt đường tròn $(O)$ tại $F$ ($F$ khác $B$).

a) Chứng minh rằng tứ giác $DHEC$ nội tiếp.

b) Kẻ đường kính $AM$ của đường tròn $\left( O \right)$ và $OI$ vuông góc với $BC$ tại $I$. Chứng minh rằng $I$ là trung điểm của $HM$.

c) Khi $BC$ cố định, xác định vị trí của $A$ trên đường tròn $(O)$ để $DH.DA$ lớn nhất.

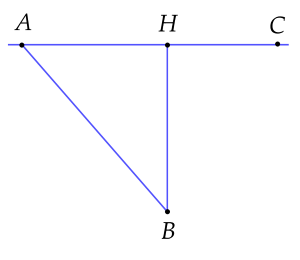
Một ô tô đang chuyển động trên đường thẳng $AC$ theo hướng từ $A$ đi về phía $C$ với vận tốc $10$ m/s, một người đứng tại $B$ cách mép đường một khoảng $BH = 50$ m. Khi khoảng cách giữa người và ô tô là $AB = 200$ m thì người đó bắt đầu chạy ra đón ô tô (coi ô tô và người chuyển động thẳng đều). Tìm vận tốc tối thiểu và hướng chạy của người tạo với $AB$ góc bao nhiêu để đón được ô tô.