Đề 4 thi thử vào 10 năm 2025 - Cấu trúc 100% trắc nghiệm

Câu 1 (1đ):

Phương trình $x^2=11$ có nghiệm là

x=11

.

x=\pm 11

.

x=121

.

x=\pm \sqrt{11}

.

Câu 2 (1đ):

Cho phương trình bậc hai một ẩn $ax^2+bx+c=0$ $(a\ne 0)$ có biệt thức $\Delta =b^2-4ac$ , phương trình đã cho vô nghiệm khi

\Delta >0

.

\Delta \ge 0

.

\Delta =0

.

\Delta \lt 0

.

Câu 3 (1đ):

Biết rằng phương trình $-3x^2+5x+1=0$ có hai nghiệm $x_1;\,x_2$ . Khi đó $x_1+x_2$ bằng

\dfrac{-5}{6}

.

\dfrac{5}{3}

.

\dfrac{-5}{3}

.

\dfrac{5}{6}

.

Câu 4 (1đ):

Thể tích hình nón có đường cao $h$ và bán kính đáy $R$ là

V= h.\pi. R

.

V=\dfrac13 h.R

.

V=\dfrac13 h.\pi. R^2

.

V= h.\pi. R^2

.

Câu 5 (1đ):

Cho $\Delta {ABC}$ vuông tại ${A}$ có $AC = 3$ ; $AB = 4$ . Khi đó $\cos B$ bằng

\dfrac{3}{5}

.

\dfrac{3}{4}

.

\dfrac{4}{5}

.

\dfrac{4}{3}

.

Câu 6 (1đ):

Khi cắt một mặt cầu tâm $O$ bán kính $R$ bởi một mặt phẳng bất kỳ thì mặt cắt thu được luôn là

hình tròn.

đường tròn.

hình chữ nhật.

hình vuông

Câu 7 (1đ):

Cho hình vẽ:

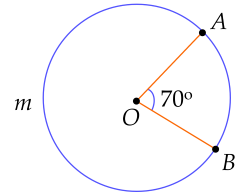
loading...

Số đo của $\overset\frown{AmB}$ trong hình bằng

140^\circ

.

290^\circ

.

110^\circ

.

70^\circ

.

Câu 8 (1đ):

Hình cầu tâm $O$ bán kính $R$ có diện tích mặt cầu là $S$ khi đó bán kính $R$ của hình cầu tính theo $S$ là

\sqrt{\dfrac{4S}{\pi}}

.

\sqrt{\dfrac{S}{4\pi}}

.

\dfrac{S}{4\pi}

.

\dfrac{4S}{\pi}

.

Câu 9 (1đ):

Cho hình vẽ, biết $AD$ là đường kính của $(O)$ , $\widehat{ACB}=76^\circ$ .

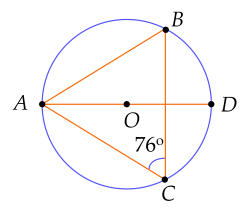
loading...

Số đo $\widehat{BAD}$ bằng

21^\circ

.

28^\circ

.

7^\circ

.

14^\circ

.

Câu 10 (1đ):

Cho mẫu số liệu ghép nhóm về thời gian gọi (phút) của một số cuộc điện thoại tại gia đình bạn Lan như sau:

Thời gian	Số cuộc gọi
$[0,5;\,2,5)$	$6$
$[2,5;\,4,5)$	$14$
$[4,5;\,6,5)$	$20$
$[6,5;\,8,5)$	$12$
$[8,5;\,10,5)$	$8$

Mẫu số liệu được chia thành bao nhiêu nhóm?

6

nhóm.

8

nhóm.

5

nhóm.

7

nhóm.

Câu 11 (1đ):

Gieo một đồng xu hai lần. Xác suất để sau hai lần gieo thì mặt sấp xuất hiện ít nhất một lần là

\dfrac{1}{3}

.

\dfrac{1}{2}

.

\dfrac{1}{4}

.

\dfrac{3}{4}

.

Câu 12 (1đ):

Cho phương trình $5x^2-3x+2=-x^2+5x-4$ . Sau khi đưa phương trình về dạng $ax^2+bx+c=0$ thì $T=a+b+c$ bằng

2

.

3

.

4

.

0

.

Câu 13 (1đ):

Tháng giêng hai tổ sản xuất được $900$ chi tiết máy; tháng hai do cải tiến kĩ thuật tổ $I$ vượt mức $15\%$ và tổ $II$ vượt mức $10\%$ so với tháng giêng, vì vậy hai tổ sản xuất được $1\,010$ chi tiết máy. Gọi số chi tiết máy mà tổ $I$ , tổ $II$ sản xuất được trong tháng giêng lần lượt là $x;\,y$ (chi tiết máy).

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Điều kiện của $x$ , $y$ là $x,\,y>0$ .
b) Phương trình biểu diễn số chi tiết máy mà cả hai tổ sản xuất được trong tháng giêng là $x+y=900$ .
c) Trong tháng $2$ , tổ $I$ sản xuất được $x+15\%x$ (chi tiết máy); tổ $II$ sản xuất được $1,1y$ (chi tiết máy).
d) Trong tháng giêng, tổ $II$ sản xuất được $500$ chi tiết máy.

Câu 14 (1đ):

Cho một số có hai chữ số. Chữ số hàng chục lớn hơn chữ số hàng đơn vị là $5$ . Nếu đổi chỗ hai chữ số cho nhau ta được một số bằng $\dfrac{3}{8}$ số ban đầu. Nếu gọi chữ số hàng chục là $a$ chữ số hàng đơn vị là $b$ .

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Điều kiện xác định $a,\,b\in \mathbb{N}$ và $a,\,b\le 9$ .
b) Biểu diễn $a$ theo b ta có: $a=b+5$ .
c) Giá trị của số mới sau khi đổi vị trí hai chữ số là $10b+a$ .
d) Số cần tìm là $83$ .

Câu 15 (1đ):

Cho hình vẽ, biết $\Delta ABC$ vuông tại $A$ , có $\widehat{ABC}=60^\circ$ , $AC=4$ cm.

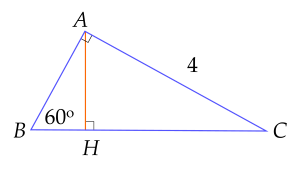
loading...

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) $\cos\widehat{ABC}=\dfrac{AB}{BC}$ .
b) $\dfrac{AH}{BH}=\dfrac{\sqrt{3}}{3}$ .
c) $\cos C=\dfrac{\sqrt{3}}{2}$ .
d) Độ dài cạnh $AH$ bằng $2\sqrt{3}$ cm.

Câu 16 (1đ):

Bảng điểm kiểm tra toán học kì $II$ của học sinh lớp 9A được cho như sau:

$8$	$8$	$9$	$10$	$6$	$7$	$10$	$6$
$10$	$5$	$7$	$8$	$8$	$4$	$10$	$8$
$10$	$8$	$6$	$10$	$9$	$7$	$6$	$9$
$9$	$10$	$7$	$8$	$5$	$10$	$8$	$8$

(Nhấp vào ô màu vàng để chọn đúng / sai)

a) Cỡ mẫu của mẫu số liệu là $N=32$ .
b) Tần số của điểm $10$ là $7$ .
c) Tần số tương đối của điểm $8$ là $25,5\%$ .
d) Tần số tương đối của điểm $7$ là $12,5\%$ .

Câu 17 (1đ):

Với mọi số thực $x$ , $y$ thì $x^2+y^2\ge a.xy$ . Giá trị của $a$ bằng bao nhiêu?

Trả lời:

Câu 18 (1đ):

Cho biểu thức $A=\dfrac{mx+n}{x^2+1}$ . Các giá trị của $m$ và $n$ để $A$ có giá trị nhỏ nhất là $-1$ , giá trị lớn nhất là $4$ . Có bao nhiêu cặp giá trị $(m,n)$ thỏa mãn?

Trả lời:

Câu 19 (1đ):

Cho biểu thức $M=\dfrac{a}{b+c}+\dfrac{b}{a+c}+\dfrac{c}{a+b}$ với $a>0;\,b>0;\,c>0$ . Giá trị nhỏ nhất của $10M$ bằng bao nhiêu?

Trả lời:

Câu 20 (1đ):

Cho $\Delta ABC$ cân tại $A$ nội tiếp đường tròn $(O)$ . Biết độ dài hai cạnh bên của $\Delta ABC$ là $6,11$ cm. $M$ là một điểm bất kỳ thuộc cung nhỏ $AC$ sao cho $AM=5,02$ cm. Tia $AM$ cắt $BC$ tại $N$ , độ dài đoạn $AN$ bằng bao nhiêu cm? (Kết quả làm tròn đến chữ số thập phân thứ hai)

Trả lời:

Câu 21 (1đ):

Tính chiều cao của cây (đơn vị mét) trong hình dưới đây, biết rằng người đo đứng cách cây $2,56$ mét và khoảng cách từ mắt người đo đến mặt đất là $1,6$ mét, góc ngắm bằng $90^\circ$ (làm tròn kết quả đến hàng phần mười).

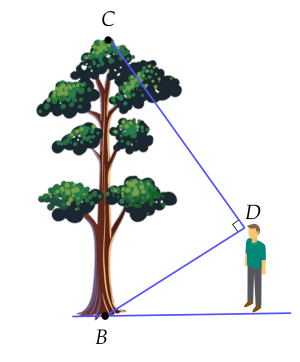
Trả lời:

Câu 22 (1đ):

Bạn Hà Gieo hai con xúc xắc $6$ mặt cân đối và đồng chất. Xác suất để tích số chấm trên mặt xuất hiện của hai con xúc xắc là một số chia hết cho $6$ bằng bao nhiêu? (Kết quả làm tròn đến chữ số thập phân thứ hai).

Trả lời:

Bài học cùng chủ đề

Đề số 3 thi thử vào 10 năm 2025 (cấu trúc 30% NLC + 40% ĐS + 30% TLN) SVIP

Yêu cầu đăng nhập!

Bài học cùng chủ đề

Báo cáo học liệu

Mua học liệu

Mua học liệu:

Số dư ví của bạn: 0 coin - 0 Xu

Nếu mua học liệu này bạn sẽ bị trừ: 2 coin\Xu

Để nhận Coin\Xu, bạn có thể:

Chi tiết xem tại đây

Thông tin của bạn

Đề số 3 thi thử vào 10 năm 2025 (cấu trúc 30% NLC + 40% ĐS + 30% TLN) SVIP

Yêu cầu đăng nhập!

Truy vết IP log

Báo lỗi câu hỏi

Các khóa học có thể bạn quan tâm

Yêu cầu VIP