Question

[DƯƠNG VĂN BÁO 11A9]

tính đạo hàm ( 3sinx - 4cosx )'

Answer 1

[quyên.]

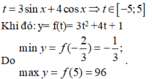
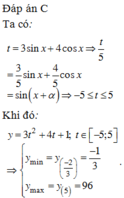
Để tính đạo hàm của hàm số \(f \left(\right. x \left.\right) = 3 sin ⁡ \left(\right. x \left.\right) - 4 cos ⁡ \left(\right. x \left.\right)\), ta sử dụng các công thức đạo hàm cơ bản:

• Đạo hàm của \(sin ⁡ \left(\right. x \left.\right)\) là \(cos ⁡ \left(\right. x \left.\right)\),
• Đạo hàm của \(cos ⁡ \left(\right. x \left.\right)\) là \(- sin ⁡ \left(\right. x \left.\right)\).

Bây giờ, tính đạo hàm từng phần:

\(f^{'} \left(\right. x \left.\right) = \frac{d}{d x} \left(\right. 3 sin ⁡ \left(\right. x \left.\right) \left.\right) - \frac{d}{d x} \left(\right. 4 cos ⁡ \left(\right. x \left.\right) \left.\right)\)

1. Đạo hàm của \(3 sin ⁡ \left(\right. x \left.\right)\) là \(3 cos ⁡ \left(\right. x \left.\right)\),
2. Đạo hàm của \(4 cos ⁡ \left(\right. x \left.\right)\) là \(- 4 sin ⁡ \left(\right. x \left.\right)\).

Vậy đạo hàm của \(f \left(\right. x \left.\right)\) là:

\(f^{'} \left(\right. x \left.\right) = 3 cos ⁡ \left(\right. x \left.\right) + 4 sin ⁡ \left(\right. x \left.\right)\)

Đáp án: \(f^{'} \left(\right. x \left.\right) = 3 cos ⁡ \left(\right. x \left.\right) + 4 sin ⁡ \left(\right. x \left.\right)\).

Chúc b học tốt nh

Answer 2

[Nguyễn Lê Phước Thịnh]

\(\left(3\cdot sinx-4\cdot cosx\right)'\)

\(=3\cdot cosx-4\cdot\left(-sinx\right)\)

\(=3\cdot cosx+4\cdot sinx\)