K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
5 tháng 5 2016
xét hàm số y=\(\sin\left(cos^2x\right)cos\left(sin^2x\right)\) =
\(\frac{sin\left(cos^2x+sin^2x\right)+sin\left(cos^2x-sin^2x\right)}{2}=\frac{sin1+sin\left(cós2x\right)}{2}\)
HA
4 tháng 4 2017
a) Cách 1: Ta có:
y' = 6sin5x.cosx - 6cos5x.sinx + 6sinx.cos3x - 6sin3x.cosx = 6sin3x.cosx(sin2x - 1) + 6sinx.cos3x(1 - cos2x) = - 6sin3x.cos3x + 6sin3x.cos3x = 0.
Vậy y' = 0 với mọi x, tức là y' không phụ thuộc vào x.
Cách 2:
y = sin6x + cos6x + 3sin2x.cos2x(sin2x + cos2x) = sin6x + 3sin4x.cos2x + 3sin2x.cos4x + cos6x = (sin2x + cos2x)3 = 1
Do đó, y' = 0.
b) Cách 1:
Áp dụng công thức tính đạo hàm của hàm số hợp
(cos2u)' = 2cosu(-sinu).u' = -u'.sin2u
Ta được
y' =[sin - sin
] + [sin
- sin
] - 2sin2x = 2cos
.sin(-2x) + 2cos
.sin(-2x) - 2sin2x = sin2x + sin2x - 2sin2x = 0,
vì cos = cos
=
.
Vậy y' = 0 với mọi x, do đó y' không phụ thuộc vào x.
Cách 2: vì côsin của hai cung bù nhau thì đối nhau cho nên
cos2 = cos2
'
cos2 = cos2
.
Do đó
y = 2 cos2 + 2cos2
- 2sin2x = 1 +cos
+ 1 +cos
- (1 - cos2x) = 1 +cos
+ cos
+ cos2x = 1 + 2cos
.cos(-2x) + cos2x = 1 + 2
cos2x + cos2x = 1.
Do đó y' = 0.
SG
0
LV
1
AH
Akai Haruma
Giáo viên
16 tháng 4 2021
Lời giải:
$y=\sqrt{\cos(x^2+2x+3)}$
$y'=\frac{-(x+1)\sin (x^2+2x+3)}{\sqrt{\cos (x^2+2x+3)}}$
NH
1
12 tháng 5 2016
\(y'=\frac{e^x}{2\sqrt{e^x}}+3.e^{3x-1}-\left(-\sin x+\cos x\right)5^{\sin x+\cos x}\ln5\)
\(=\frac{\sqrt{e^x}}{2}+3e^{3x-1}+\left(\sin x+\cos x\right).5^{\sin x+\cos x}\ln5\)
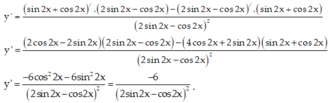
Ta cần tính đạo hàm của hàm số:
\(f \left(\right. x \left.\right) = \left(cos \right)^{2} x\)
Bước 1: Sử dụng quy tắc chuỗi
Viết lại hàm dưới dạng:
\(f \left(\right. x \left.\right) = \left(\right. cos x \left.\right)^{2}\)
Lấy đạo hàm theo quy tắc chuỗi:
\(\frac{d}{d x} \left(\right. \left(cos \right)^{2} x \left.\right) = 2 cos x \cdot \frac{d}{d x} \left(\right. cos x \left.\right)\)
Biết rằng:
\(\frac{d}{d x} \left(\right. cos x \left.\right) = - sin x\)
Thay vào ta có:
\(f^{'} \left(\right. x \left.\right) = 2 cos x \cdot \left(\right. - sin x \left.\right)\)
Bước 2: Kết quả
\(f^{'} \left(\right. x \left.\right) = - 2 cos x sin x\)
Bước 3: Viết lại theo công thức lượng giác
Ta có công thức:
\(sin 2 x = 2 sin x cos x\)
Do đó:
\(f^{'} \left(\right. x \left.\right) = - sin 2 x\)
Kết luận
\(\frac{d}{d x} \left(\right. \left(cos \right)^{2} x \left.\right) = - sin 2 x\)
Đạo hàm của cos²x là -sin 2x.