Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Thể tích ly 1 là:
V1=15^2*20*3,14=14130(cm3)
Thể tích ly 2 là:
V=20^2*12*3,14=15072(cm3)
Vì V1<V2 nên nước sẽ không bị tràn ra ngoài

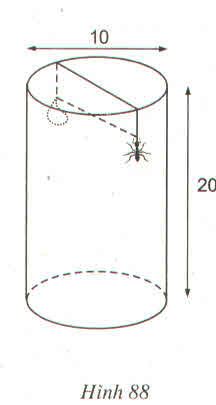
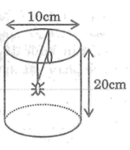
Khai triển hình trụ theo một đường sinh và trải phẳng ra ta được một hình chữ nhật có chiều rộng 20cm ,chiều dài bằng chu vi đáy của cái lọ: 10.3,14=31,4 (cm)
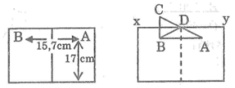
Theo đề bài, khi con kiến ở điểm A (hình dưới) cách đáy 17cm thì giọt mật ở điểm B cũng cách đáy 17cm.Khi đó con kiến cách giọt mật một khoảng cách bằng nửa chu vi đáy của cái lọ: 31,4 : 2 = 15,7 (cm)
Dựng điểm C đối xứng với B qua đường xy ,nối AC cắt xy tại D.Điểm D là điểm con kiến bò qua miệng của cái lọ đê vào bên trong thì đoạn đường BDA là ngắn nhất
Khai triển hình trụ theo một đường sinh và trải phẳng ra ta được một hình chữ nhật có chiều rộng 20cm ,chiều dài bằng chu vi đáy của cái lọ: 10.3,14=31,4 (cm)

Giải
Thể tích của tượng đá bằng thể tích của hình trụ có diện tích đáy là 12,8 cm2 và chiều cao bằng 8,5 mm = 0,85 cm vậy:
V = S.h = 12,8.0,85 = 10,88 cm3

Bài 1:
Gọi số học sinh trong tổ là \(x\left(x>2\right)\)
Số tiền mỗi người dự định phải đóng: \(\frac{72}{x}\) (ngàn đồng)
Số tiền thực tế mỗi người phải đóng: \(\frac{72}{x-2}\) ngàn đồng
Ta có phương trình:
\(\frac{72}{x-2}-\frac{72}{x}=3\Leftrightarrow72x-72\left(x-2\right)=3x\left(x-2\right)\)
\(\Leftrightarrow3x^2-6x-144=0\Rightarrow\left[{}\begin{matrix}x=8\\x=-6< 0\left(l\right)\end{matrix}\right.\)
Bài 2:
Thể tích bình thứ nhất: \(V_1=\pi R_1^2h_1=\pi.15^2.20=4500\pi\left(cm^3\right)\)
Thể tích bình thứ 2: \(V_2=\pi R^2_2h_2=\pi.20^2.12=4800\pi\left(cm^3\right)\)
Do \(V_2>V_1\) nên nước ko bị tràn

Giả sử khi chảy một mình thì vòi thứ nhất chảy đầy bể trong x phút, vòi thứ hai trong y phút. Điều kiện x > 0, y > 0.
Ta có 1 giờ 20 phút = 80 phút.
Trong 1 phút vòi thứ nhất chảy được \(\frac{1}{x}\) bể, vòi thứ hai chảy được \(\frac{1}{y}\) bể, cả hai vòi cùng chảy được \(\frac{1}{80}\) bể nên ta được \(\frac{1}{x}+\frac{1}{y}=\frac{1}{80}\).
Trong 10 phút vòi thứ nhất chảy được \(\frac{10}{x}\) bể, trong 12 phút vòi thứ hai chảy được \(\frac{12}{x}\) bể. Vì cả hai vòi cùng chảy được \(\frac{2}{15}\) bể. Ta được:
\(\frac{10}{x}+\frac{12}{x}=\frac{2}{15}\)
Ta có hệ phương trình: \(\begin{cases}\frac{1}{x}+\frac{1}{y}=\frac{1}{80}\\\frac{10}{x}+\frac{12}{y}=\frac{2}{15}\end{cases}\)
Giải ra ta được x = 120, y = 240.
Vậy nếu chảy một mình, để đầy bể vòi thứ nhất chảy trong 120 phút (2 giờ), vòi thứ hai 240 phút (4 giờ).



a) Thể tích nước trong lọ thứ nhất:
Lọ hình trụ → \(V = \pi r^{2} h\)
\(V = 3,14 \times 7^{2} \times 8 = 3,14 \times 49 \times 8 = 3,14 \times 392 = 1230,88 \textrm{ } \text{cm}^{3}\)
a: 1230,88 cm³
b) Thể tích lọ thứ hai:
\(V = 3,14 \times 8^{2} \times 6 = 3,14 \times 64 \times 6 = 3,14 \times 384 = 1205,76 \textrm{ } \text{cm}^{3}\)
Vì 1230,88 > 1205,76, nên nước sẽ bị tràn ra ngoài.
b: Bị tràn vì thể tích lọ thứ hai nhỏ hơn thể tích nước đổ vào.