Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Em kiểm tra lại đề, \(\left(\alpha\right)\) đi qua AI nên nó không thể cắt SA tại M được nữa (vì nó đi qua A nên đã cắt SA tại A rồi)

Bài này cũng có thể ứng dụng bài này (vẫn là sử dụng diện tích tam giác):
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Giả sử mp (a) cắt SA; SB;SC; SD thứ tự tại A' B' C' D'. Tính \(\dfra... - Hoc24
Nhưng đặc biệt hơn 1 chút là nó đi qua điểm A luôn (vậy ta có thể coi như (P) cắt SA tại A và áp dụng nó vẫn đúng):
\(\dfrac{SA}{SA}+\dfrac{SC}{SP}=\dfrac{SB}{SN}+\dfrac{SD}{SQ}=\dfrac{2SO}{SI}=8\)
\(\Rightarrow1+\dfrac{SB}{SN}+\dfrac{SC}{SP}+\dfrac{SD}{SQ}=16\)
\(\Rightarrow\dfrac{SB}{SN}+\dfrac{SC}{SP}+\dfrac{SD}{SQ}=15\)

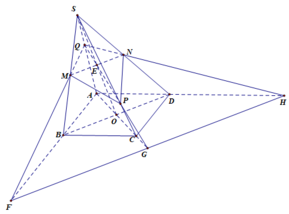
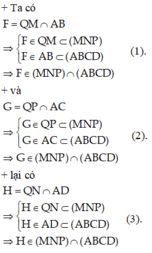
Từ (1) (2) và (3) suy ra ba điểm F, G, H thuộc giao tuyến của hai mặt phẳng (MNP) và (ABCD).
Do đó ba điểm F, G, H thẳng hàng và G nằm giữa F và H.
Chọn C.
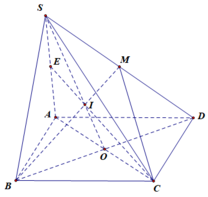

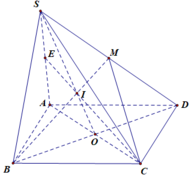


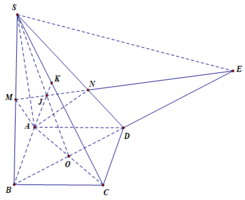
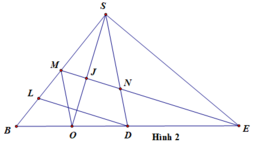
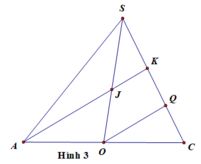


Nối AN kéo dài cắt CD tại E, nối EM kéo dài cắt SD tại I
Do N là trung điểm OB \(\Rightarrow\dfrac{BN}{ND}=\dfrac{1}{3}\)
Áp dụng định lý talet: \(\dfrac{BF}{AD}=\dfrac{BN}{ND}=\dfrac{1}{3}\) \(\Rightarrow\dfrac{CF}{AD}=\dfrac{2}{3}\)
Cũng theo Talet:
\(\dfrac{FC}{FD}=\dfrac{CF}{AD}=\dfrac{2}{3}\) \(\Rightarrow\dfrac{DF}{FC}=\dfrac{3}{2}\)
Áp dụng định lý Menelaus cho tam giác SCD:
\(\dfrac{IS}{ID}.\dfrac{DF}{FC}.\dfrac{CM}{MS}=1\Rightarrow\dfrac{IS}{ID}.\dfrac{3}{2}.1=1\Rightarrow\dfrac{IS}{ID}=\dfrac{2}{3}\)
\(\Rightarrow\dfrac{SI}{SD}=\dfrac{2}{5}\)